If the bulk modulus were negative, the system would be in an unstable configuration. (Thermodynamically, this means that it is not a minimum of the free energy. However, the instability is really just purely mechanical; no references to $S$ and $T$ are requried.) Consider a system (for simplicity and definiteness, make it a fluid) with negative bulk modulus $B$ at a given pressure $P$ and volume $V$. What happens if we compress (by applying an external force) the system, so that $V\rightarrow V+\Delta V$, with $\Delta V<0$?
If $B$ is negative, then the pressure drops by a positive amount, $|\Delta P|$, where the actual $\Delta P<0$. In a realistic system, the pressure would increase as the system is compressed, so that it would eventually come back to equilibrium, when the increased pressure balances the applied external force. However, here the volume decreases and the pressure drops, which means that as the system shrinks, it becomes less and less able to resist the external force, meaning that it will continue to shrink even more! The reverse happens if we start out by allowing the system to expand a little and increase its pressure, which would cause it to expand even further. Either way, a miniscule change in volume leads to a runaway effect, with volume either increasing or decreasing until the equation of state changes enough to make $B$ positive again.
It is possible, in principle, to have a nonequilibrium system with a negative $B$, but the configuration is unstable. For example, direct application of the van der Waals equation of state,
$$\left(P+\frac{an^{2}}{V^{2}}\right)(V-nb)=nRT,$$
predicts than when $T$ is small enough (less than the critical point temperature $T_{c}$) there a region where the bulk modulus is negative (as shown in this image from Wikipedia).
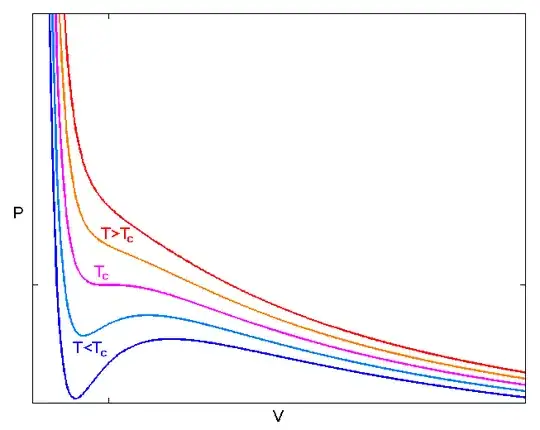
If a fluid is quickly supercooled into the region with negative $B$, the anomalous behavior can be directly observed, but only briefly. What happens after a very short period of time is that the instabilities take over. Some regions of the fluid (where the local pressure happened to be lower) rapidly expand and other regions (where the pressure was randomly a little higher) rapidly contract. These become regions of gas and liquid, respectively! The instability is resolved by a phase separation; a system with negative $B$ has greater free energy than the same system split into separate liquid and gas components.
