Why is it that we can think of a symmetrical wheel as rotating about an "instantaneous" axis of rotation passing through point of contact with ground?

Question

Consider the situation of combined translation and rotation that is represented by a symmetrical wheel that is rolling without slipping.

In the book "University Physics", 14th Ed., page 311 there is the following snippet

At any instant we can think of the wheel as rotating about an “instantaneous axis” of rotation that passes through the point of contact with the ground. The angular velocity v is the same for this axis as for an axis through the center of mass; an observer at the center of mass sees the rim make the same number of revolutions per second as does an observer at the rim watching the center of mass spin around him.

I can not understand this notion that the wheel can be thought of as rotating about an instantaneous axis passing through the point of contact with the ground.

Here is what I understand

The wheel not slipping seems to mean that the point of contact with the ground has zero velocity relative to the ground. In this other question, the second answer provides a nice way to think about this when it tells us to imagine a star-shape with n edges rolling. The point in contact with the ground has zero velocity.

While one particular point of an edge on such a star shape is in contact with the ground, it seems that the entire shape is indeed rotating about the axis through that point.

If this is the correct analogy for the case with "infinite edges" that is a circle rolling, it is bewildering why the book did not motivate the statement of this with any sort of intuition.

For additional context on this question, here is the text of the entire section that appears before the snippet above

Rolling Without Slipping

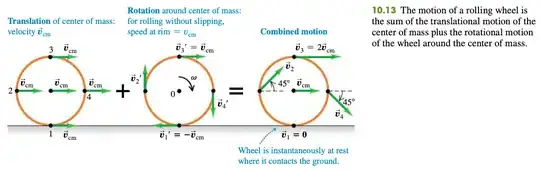
An important case of combined translation and rotation is rolling without slipping. The rolling wheel in Fig. 10.13 is symmetrical, so its center of mass is at its geometric center. We view the motion in an inertial frame of reference in which the surface on which the wheel rolls is at rest. In this frame, the point on the wheel that contacts the surface must be instantaneously at rest so that it does not slip. Hence the velocity $\vec{v}'_1$ of the point of contact relative to the center of mass must have the same magnitude but opposite direction as the center-of-mass velocity $\vec{v}_{cm}'$. If the wheel’s radius is $R$ and its angular speed about the center of mass is $v$, then the magnitude of $\vec{v}_1'$ is $R\omega$; hence

Condition for rolling without slipping: $v_{cm}=R\omega$

As Fig. 10.13 shows, the velocity of a point on the wheel is the vector sum of the velocity of the center of mass and the velocity of the point relative to the center of mass. Thus while point 1, the point of contact, is instantaneously at rest, point 3 at the top of the wheel is moving forward twice as fast as the center of mass, and points 2 and 4 at the sides have velocities at 45° to the horizontal.

And here is the cited Figure 10.13

Answer 1

A useful example of this is a wheel on a tilted ramp. Angular velocities must be the same. Consider a line drawn from the surface to the center of the wheel at a certain time. In the ground frame of reference, the bottom has zero velocity and the top has the velocity of the wheel's center. In the wheel's center frame of reference, the top has zero velocity and the bottom has the velocity of the wheel's center in the opposite direction. In the question's picture, the line's angular velocity would be clockwise in both frame's of reference. The magnitude of the angular velocity would be the wheel speed divided by the wheel radius in both cases. As a result, angular velocity would have to be the same in both cases.

Now consider force and torque causing this acceleration. The wheel feel's three forces. The weight is at the wheel's center, pointed downward. Normal force and friction are at the point of contact, perpendicular and parallel to the tilted ramp. With the point of contact as the pivot, you have purely rotational motion for that instant of time. The friction and normal force do not contribute torque. The net torque is from the weight: $\tau = I\alpha$ with the center of mass around the pivot. $I=I_{cm}+MR^2$. The torque is $\tau=RMg\sin(\theta)$, with $\theta$ as the ramp's tilt. The acceleration of the wheel's center of mass is $a=R\alpha$. These then go together to make $RMg\sin(\theta)=(I_{cm}+MR^2)\alpha$.

If you use the center of mass as the pivot, the net force is the component of weight parallel to the ramp minus the friction: $F=Mg\sin(\theta)-f=Ma$. Only the friction contributes to angular acceleration, so torque around the center of mass is $Rf=I_{cm}\alpha$. If you put these together, $RMg\sin(\theta)-Rf=RMa=MR^2\alpha$. Substitute in the expression for $Rf$ and you get $RMg\sin(\theta)=I_{cm}\alpha+MR^2\alpha$.

The relation between force, radius, and angular acceleration is the same in both frames of reference.