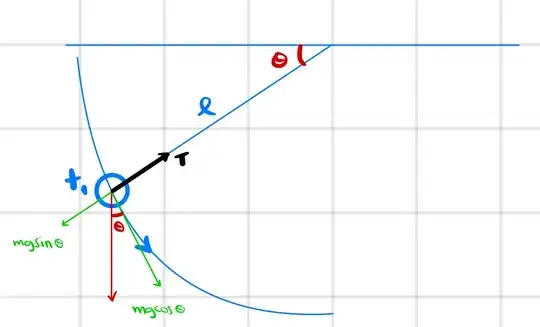
Consider a pendulum of mass $m$ and length $l$, released from rest in a horizontal position. At some time $t_1>t_0=0$, the situation looks like the following
I am aware that we can use conservation of energy to figure out the speed of the mass.
$$E_{mech}(t_0)=U_0+K_0=mgl$$
$$E_{mech}(t_1)=U(t_1)+K(t_1)=mg(l-l\cos{\theta})+\frac{mv^2}{2}$$
$$\implies v=\sqrt{2gl\cos{\theta}}$$
However, what I'd like to do is compute the change in linear momentum using impulse by considering my system to be just the mass. Tension on the pendulum string and gravitational force are thus external to the system, and an impulse by these forces should give us the change in momentum of the mass.
$$\int_{t_0}^{t_1} F^{ext}(t)dt=\int_{t_0}^{t_1} \left [ (mg\sin{\theta(t)}-T)\hat{r}+mg\cos{\theta(t)}\hat{\theta} \right ]dt$$
Note that $\hat{r}$ and $\hat{\theta}$ are functions of $t$, and we know the functional form because we can express these vectors in the Cartesian basis using $\theta(t)$.
$$\int_{t_0}^{t_1} F^{ext}(t)dt=\int_{t_0}^{t_1} \left [ (mg\sin{\theta(t)}-T(t))(-\cos{\theta(t)}\hat{i}-\sin{\theta(t)}\hat{j})+mg\cos{\theta(t)}(\sin{\theta(t)}\hat{i}-\cos{\theta(t)}\hat{j}) \right ]dt$$
$$=\int_{t_0}^{t_1} T(t)\cos{\theta(t)}dt\ \hat{i}+\int_{t_0}^{t_1} [T(t)\sin{\theta(t)}-mg]dt\ \hat{j}\tag{1}$$
$$=\Delta p = m\vec{v(t_1)}$$
We don't know what $\theta(t)$ and $T(t)$ are at this point, however, so we can't integrate.
In the $\hat{\theta}$ direction, Newton's 2nd law says
$$mg\cos{\theta(t)}=ma_T=mr\alpha(t)$$
$$\alpha(t)=\theta''(t)=\frac{g\cos{\theta(t)}}{r}$$
$$r\alpha(t)=g\cos{\theta(t)}\tag{2}$$
In the $\hat{r}$ direction we have
$$(mg\sin{\theta}-T(t))\hat{r}=ma_R=m(-l\theta'(t)^2)\hat{r}$$
$$T(t)-mg\sin{\theta}=ml\theta'(t)^2$$
My questions are
Are these calculations correct so far?
Is (2) a nonlinear differential equation?
How do we solve the integrals in (1)?