Does the formula for time period of a simple pendulum hold up for larger angles?

Question

When calculating the time period of a simple pendulum as an experiment in junior classes we used the formula $$T = 2\pi\sqrt{\frac{l}{g}}$$

But recently seeing the derivation of the formula using Simple Harmonic Motion, I can't understand how it holds for such large angles since $\sin{\theta}$ gets approximated to $\theta$ which only holds true for very small values of $\theta$ (or as it would be written mathematically for $\theta \to 0$).

So, how, if at all, does this formula hold for the larger angles and why is it used for calculating time period of a pendulum during experiments?

Answer 1

If you want to have an idea how far the result deviates from its small-angle approximation…

The pendulum's total energy is: $$E=K+V=\frac{1}{2}m(l\dot{\theta})^2-mgl\cos(\theta)$$ Let's assume that the pendulum starts from an angle $\theta_0$ with no velocity. Conservation of energy yields: $$\dot{\theta}^2=2\frac{g}{l}\bigl(\cos(\theta)-\cos(\theta_0)\bigr)$$ During the half-period where the pendulum swings from $-\theta_0$ to $\theta_0$, its angular velocity $\dot{\theta}$ is positive, so the half-period is: $$\frac{T}{2} =\int_0^{\frac{T}{2}}dt =\int_{-\theta_0}^{\theta_0}\frac{d\theta}{\dot{\theta}}$$ which yields: $$T=2\sqrt{\frac{2l}{g}}\int_0^{\theta_0}\frac{d\theta}{\sqrt{\cos(\theta)-\cos(\theta_0)}}$$ This integral can be computed numerically. Here's a graph of the period versus $\theta_0$:

As you can see, the approximation $T\simeq 2\pi\sqrt{\frac{l}{g}}$ keeps some validity until 1 to 2 rad.

Answer 2

The exact solution is given by this equation:

$$T=4\,\sqrt{\frac lg}\int_0^{\pi/2}\frac{d\vartheta}{\sqrt{1-k^2\,\sin^2(\vartheta)}}\tag 1$$

where $~k=\sin(\theta_0/2)~$ and $~\theta_0~$ is the pendulum start amplitude.

Thus if $~\theta_0=0~$ you obtain that period $~T_L=2\pi\sqrt{\frac lg}$

This graph gives you period $~\frac{T}{T_L}~$ via the pendulum start amplitude:

Thus (for example) for $\theta_0=50~$ degrees the pendulum period is 5% greater than the approximation $~T_L~$.

Answer 3

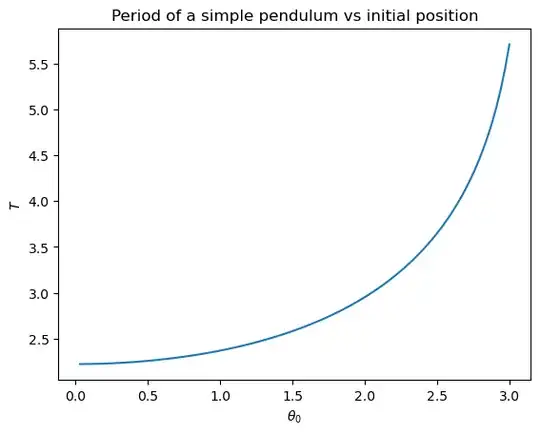
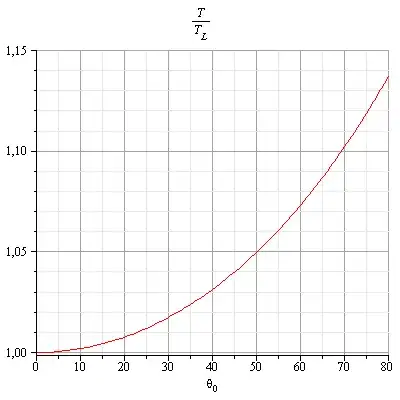
Miyase's answer shows how to calculate the period for larger oscillations, and shows that it's no longer $T = 2 \pi \sqrt{l/g}$. But you also asked the following question that I wanted to address:

[W]hy is it used for calculating time period of a pendulum during experiments?

And the basic answer I would give is: "Every time you design an experiment, you have carefully consider what you can neglect. For many purposes, this result is 'good enough'."

Let's suppose that your goal is to measure the period of a pendulum and compare it to the predicted value from Newtonian mechanics. It's true that Newtonian mechanics says that the period of a physical pendulum is not exactly $2 \pi \sqrt{l/g}$; for an amplitude of 10°, it deviates from that by about 0.2%. There's a nice calculator here if you want to play around with how big these deviations are for other amplitudes.

But if other factors in the experiment mean that you can practically only measure the period of the pendulum to within 1%, then you're never going to measure that small deviation from the "ideal" behavior and so you can neglect it. If, on the other hand, you have a very precise period measurement, and you can reliably measure the period to within 0.01%... well, maybe you'll need to know the more precise formula. But you'll also have to have:

• a more reliable measure of local gravity than the standard value of $9.8\text{ m/s}^2$, since $g$ varies by about 0.5% over Earth's surface.
• A precise measurement of the position of the center of gravity and the moment of inertia of your pendulum bob. These can be tricky to get to high precision, and indeed there are clever pendulum designs that allow you to avoid having to locate the center of gravity to such precision.
• Some kind of justification that the effects of friction in the pendulum bearing, and of air resistance, are small (you'd want a very high Q factor). Otherwise the period will again deviate from the "ideal" value.

And myriad other factors. You can see why we don't bring all of these considerations into the lab exercises during junior classes; but the instructors who designed them presumably thought about them, and (hopefully) would have told you all this if you had asked them this question at the time.

Answer 4

That formula is not valid for large oscillations because as you point out, the small angle trick no longer holds- but it works just fine as an approximation to the behavior of penduli in physics laboratories, which is why we use it there. For large angles, the sin function must be explicitly included in the dynamical description of the pendulum and the resulting math becomes very difficult.

Note in any case that even for large angles, the pendulum itself still oscillates with a well-defined period (i.e., it still works like a clock!)- it's just that in the large-angle case, the period depends on the amplitude.