Some sources on the web claim that "electricity follows the path of least resistance" is not true, e.g. this physics SE question. However, in every explanation of "short circuits", the author says that current flows through the short because it's following the path of least resistance. How do I reconcile these two facts?
Asked
Active
Viewed 1.0k times
2 Answers
4
It's more like "Electricity tries to follow the path of least resistance". The sentence is a non-rigorous intuitive tool that helps one quickly make sense of current paths. It's not a physical law.
This comes from the behavior of resistors in parallel --this is where current has a "choice" of which direction to take. The potential difference across a resistor is equal to the current into its resistance ($V=IR$, usually called Ohm's law) in appropriate units.
What happens when you have two resistors in parallel is that the p.d. across them must be the same. Which means that $I_1R_1=I_2R_2$. So, more current flows through the resistor with less resistance and vice versa. Current still flows through the greater resistance.
So most current flows through the path of least resistance. In the case of a short circuit, one of the Rs is (nearly) zero, and thus (almost) all the current flows through it.
Manishearth
- 19,167
- 6
- 64
- 104
4
The statement electricity flows through the path of least resistance means that electricity flows more into the path with less resistance, because it is proportional to the inverse of resistance, obeying:
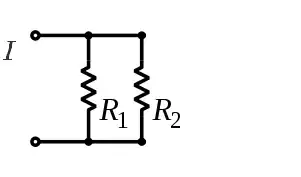
$$I_1=I\frac{R_2}{R_1+R_2}$$ $$I_2=I\frac{R_1}{R_1+R_2}$$
From these relations you can find out that in two cases all of the current flows through the 1st resistor:
- $R_1=0$
- $R_2\gg R_1$ $($mathematically $R_2\to\infty$ $)$
The important fact is that what matters here is the ratio of the resistances: $$I_1=I\frac{R_2}{R_1+R_2}\to I_1=I\frac{1}{\frac{R_1}{R_2}+1}$$
If you plot $I_1\over I$ from the above relation (w.r.t $\frac{R_1}{R_2}$ ) you can see this better:
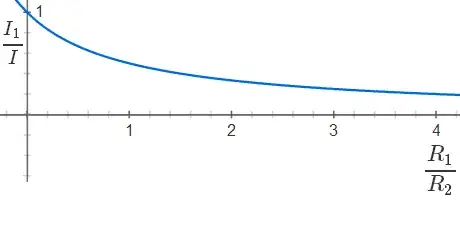
This is the meaning of the quoted statement.
Mostafa
- 4,034