How do electrons move?

Question

Are they spinning around the nucleus? If so what makes them move? I just do not understand how they move or if they are "attracted" to something is it another particle that makes it move.

Answer 1

The electron is an elementary particle, bound by the rules of Quantum Mechanics.

It is not a particle like a tiny billiard ball, it is a quantum mechanical entity which sometimes does have mass and a position in spacetime (x,y,z,t) and sometimes it manifests as a probability wave in dimensions commensurate to h, the Planck constant . The boundary conditions of the problem define which will be the manifestation, particle or probability wave, when a measurement is made of a particular electron.

This means that when an electron is free , not in a potential well, measurements will show a track defining a classical trajectory of its motion.

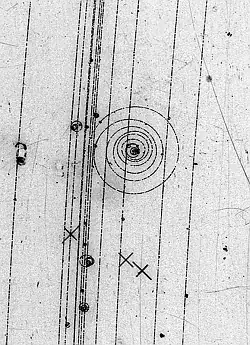
Bubble chamber photograph of an electron knocked out of a hydrogen atom

The electron you see knocked off before the knock was in an orbital around the proton nucleus of the hydrogen atom. An orbital, not an orbit, because its location is probable, described by a probability wave given by a mathematical formula, the square of the wavefunction which is a solution of the potential problem "electron and proton in the field of each other".

The shapes of the first five atomic orbitals: 1s, 2s, 2px, 2py, and 2pz. The colors show the wave function phase. These are graphs of ψ(x, y, z) functions which depend on the coordinates of one electron. To see the elongated shape of ψ(x, y, z)2 functions that show probability density more directly, see the graphs of d-orbitals below.

So the electron in its previous life was not orbiting the proton, the way the moon orbits the earth, but it had a probability of being in a particular (x,y,z) when probed.

So in the image, the electron moves because another particle kicked it and transferred momentum enough to free it from the proton of the hydrogen atom. When in a orbital it is in a steady state situation, except its position is undefined within the limits given by the probability derived from the wavefunction, which depends on the potential in the problem.