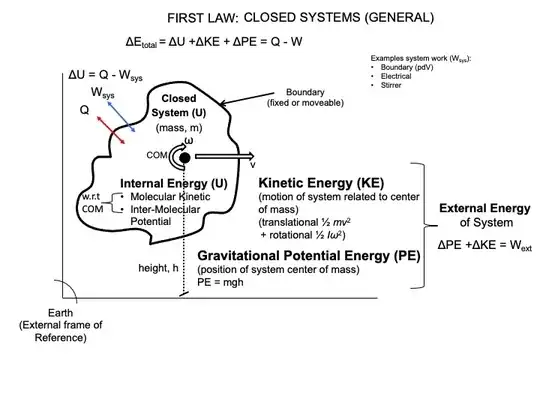
I'm starting in the field of thermodynamics and I'm seeing that in the formulation of the first law, we only take care of the internal energy but not in the energy of the whole system. Let me explain:
The energy of a system can be written as $E_{system}=K_{system}+U_{system}$ when dealing with a system of particles, $K_{system}=\sum K_i=\sum\frac{1}{2}m_iv_i^2$ and $U_{system}=\sum U_i$. But we know that $K_{system}=\frac{1}{2}m_Tv_{cm}^2+\sum\frac{1}{2}m_iu_i^2$, where $m_T$ is the total mass of the system, $v_{cm}$ is the speed of the center of mass, and $u_i$ is the speed of the $i$-th particle with respect to the center of mass. This means that the internal energy can be expressed as $\mathcal{U}=\sum\frac{1}{2}m_iu_i^2+\sum U_i$, and so the energy of a system $E_{system}=\frac{1}{2}m_tv_{cm}^2+\mathcal{U}$.
When aplying the conservation of energy principle to the system when no heat is considered, $W_{ext}=\Delta E_{system}=\Delta\left(\frac{1}{2}m_tv_{cm}^2\right)+\Delta\mathcal{U}$, which means that external work produces changes both in the internal and center of mass energy.
Now let's take heat in consideration. A similar expression may be written: $W_{ext}+Q=\Delta E_{system}=\Delta\left(\frac{1}{2}m_tv_{cm}^2\right)+\Delta\mathcal{U}$, but comparing it with the first law of thermodynamics, there is an extra term, $\Delta\left(\frac{1}{2}m_tv_{cm}^2\right)$, because, as far as I know, the first law of thermodynamics is formulated as $W_{ext}+Q=\Delta\mathcal{U}$.
My question is why we don't write the term $\Delta\left(\frac{1}{2}m_tv_{cm}^2\right)$ in the first law of thermodynamics? Is it that I have misconceptions in some of the concepts used here, or is it that, for example, in thermodynamics we always work in a reference frame moving with the center of mass of the system, making $v_{cm}=0$ always, or what's the issue I'm having here?
Thank you.