Why does the doubly-magic nucleus tin-$132$ have such a short mean lifetime?

Question

Why does the doubly-magic nucleus tin-$132$ have such a short mean lifetime? Only because it is far from valley of stability?

Answer 1

At first, heaviest unstable $Sn$ isotope found is not ${}^{132}Sn$, but ${}^{139}Sn$, having 89 neutrons with half-life of $130~\text{ms}$.

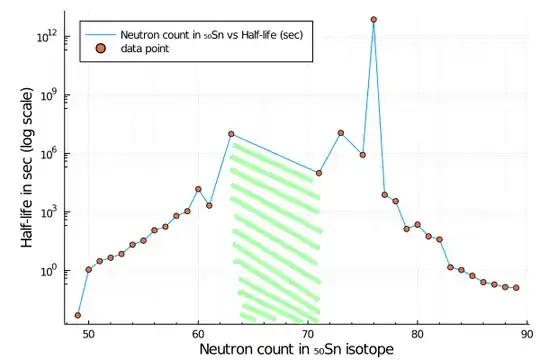
Second, if you'll draw a chart how half-life depends on number of neutrons in a Tin, you'll get this:

Stability band is between $N \in [63,71]$, where neutron amount is roughly about $[1.3,1.4]\times Z$, i.e. when neutron number not exceeds proton number very much, so that repulsive electrostatic force between protons is balanced nicely with strong nuclear force.

If there is too much neutrons, then nucleus becomes unstable, so that either $\beta^-$ or $\beta^+$ decay happens, converting either protons into neutrons or vise-versa - neutrons into protons, with reactions :

$$ n \to p + e^- + \overline \nu_e \\ p \to n + e^+ + \nu_e \tag 1$$

Finally, just for the sake of argument, if there's too less neutrons,- so that according to liquid drop model,- when neutron number in nucleus will be :

$$ N \leq \frac {1}{47}Z^2 −Z \tag 2,$$

then Spontaneous fission will happen noticeably.

For ${}_{50}Sn$ (2) gives just 3 neutrons. In spontaneous fission nucleus starts to emit heavy particles like in $\alpha$ decay. However, it's not easy to artificially build ${}^{53}_{50}Sn$ isotope to test this neutron lower bound condition. From the rest of known all elements and their isotopes, just ${}^{294}_{118}Og$ element have required condition :

$$ Z^2/A = 47.36 \geq 47 \tag 3$$ for spontaneous breakout (at least in the liquid drop model which is not too accurate for heavy atoms).

Nevertheless,- neutron number in a nuclei must have right balancing conditions to a proton number, so that less or more neutrons is hazard for an atom in general.