How do astronomers measure the angle p?
"Instead of closing one eye and then the other, we observe a star six months apart, so that we are on opposite sides of the sun for each observation. Watch the star shift against background star field, and measure that shift. Define the parallax angle as half this shift."
Why does the shift measurement (which is a length) match the angle measurement or at least has any relation to the parallax angle measurement? Is this related to a change of coordinates?
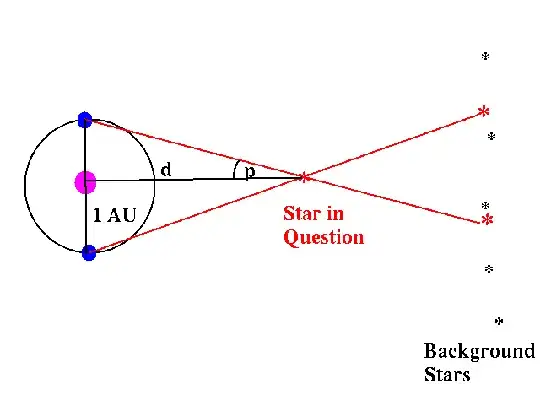
The shift measurement isn't a length, it is an angle. The position of a star on the sky is specified with two angles - just like spherical polar coordinates. If a star "moves" with respect to this coordinate system, defined by very distant quasars that are assumed to be fixed, then these angles change and the apparent motion of the star on the sky is an angular displacement.
In terms of how a parallax is measured, the cartoon shown in all textbooks is vastly simplified. A more realistic view is that the position of a star is measured several times over the course of years. The annual parallax causes the star to trace out an ellipse on the sky against the fixed coordinate system. Fitting the parameters of the ellipse gives the parallax angle because the shape and size of the ellipse depends on the star's position and parallax.
Reality is more complicated again though, because stars also have "proper motion" within the Galaxy with respect to the Solar System. This means their positions in the sky drift with time. This motion must also be combined into the model using a "5-parameter astrometric fit" - the two angles specifying position at some epoch, the parallax, and two proper motion rates in the two angular directions.
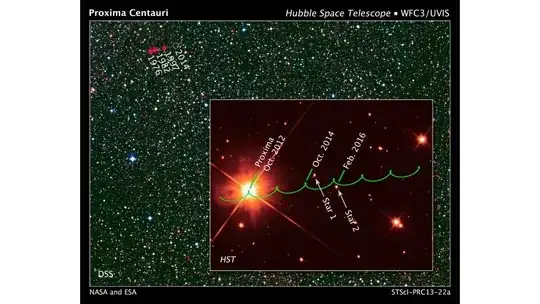
An exaggerated example is shown below, illustrating the combined parallax and proper motion displacement on the sky of the nearby star Proxima Centauri. The other stars in the picture are much more distant and approximate the fixed coordinate reference frame. The proper motion is the big, linear drift in position from year to year. The component of motion due to parallax are the the little "up-ticks" in the track that repeat every year.
How astronomers measure the parallax angle and how it relates to an actual length are really two separate questions.
The sky can be divided up into 360 degrees or $2\pi$ radians. If two objects are apart by some fraction of the sky, treating the sky as a sphere, then the angle is that fraction times 360 degrees or $2\pi$ radians. As a simple example, the Sun in your diagram would be on opposites sides of the sky at the two points, half the sky apart, so the angle would be $\pi$ radians or 180 degrees.
From your diagram, after measuring the parallax angle, $\tan p = \frac{1 AU}{d}$, or $d = \frac{1 AU}{\tan p} \approx \frac{1 AU}{p}$. The last bit is if $p$ is measured in radians, since $\tan p \approx p$ for small angles. This is using trigonometry. As a fun note, this is where the term "parsec" is from: a Parallax of an Arcsecond corresponds to a Parsec, $\rm{parsec} = \frac{1 AU}{\rm{arcsecond~in~radians}}$. There are 60 arcminutes in a degree and 60 arcseconds in an arcminute, so 3600 arcseconds in a degree.
