Following from this question, I am now confused how clocks of one observer is turning into disagreement with that of another. I have seen a mathematical explanation here, but what is the physical explanation of how one clock starts ticking slower than another?
Relevant to answering this maybe the Andromeda paradox.
The easiest way to understand time dilation and length contraction is to examine the same effects in ordinary Euclidean geometry. The analogy is not exact, but it gives the intuition a starting point that can be adjusted with the mathematical details.
Consider two people walking at the same speed but in slightly different directions across a field. Each of them defines their own coordinate system consisting of 'forwards' and 'sideways' directions. Because they are moving forwards at a constant rate, this stands in as a proxy for time. 'Sideways' then stands in for the spatial dimensions.
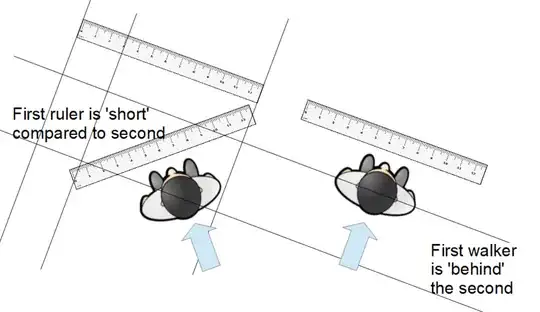
We look at the forwards-sideways coordinate system of the walker on the right. He lays a ruler sideways to measure space, and counts steps forwards to measure ticks of time. He glances at his companion to the left. His companion has his own ruler, laid out 'sideways', but his 'sideways' is tilted! The result is that the distance between the ends of his neighbour's ruler according to his own coordinate system is shorter than it should be. Likewise, his companion has fallen slightly behind. He appears to be moving more slowly across the field, the 'ticks' of his footsteps are closer together than they should be.
The walker on the left, looking at his companion on the right, says exactly the same things. The ends of his friend's ruler are too close together in the 'sideways' direction. He is moving 'forwards' at a slower rate. They can both see the other as shrunk in space and falling backward in time because they are each using different definitions for sideways/forwards corresponding to space/time.
The moving clock does not 'tick slower' - it is because its ticks are being measured along a different direction in spacetime. The ticks themselves haven't changed - what has changed is our choice of definitions of time and space.
The two different meanings of time in special relativity correspond to the two different meanings of 'distance' in Euclidean geometry. Say we move along some curvy winding path to the point 3 miles east and 4 miles north of where we started. How far have we walked? Well, if we just look at the distance north we have travelled, this is 4 miles. This is like the coordinate time. We have to specify a particular coordinate system, and every point has a well-defined distance from the starting point. But if we switch to a different coordinate system (magnetic north instead of true north, say) then the answer will change. The other way to look at it is the length of the curvy path we actually walked along. This corresponds to the proper time, and is the time a moving observer will experience, and is the time shown by a clock he carries with him (counting steps). The 'proper time' length for a path is the same in any coordinate system. It doesn't matter if you use magnetic north or true north or north-east and south-west as your coordinate directions - if you walked 7 miles in one coordinate system, it's 7 miles in all of them. However, there is no longer a well-defined 'distance' between points - it depends what route you took. So I might have walked 7 miles, but my twin brother walked a different route and has travelled 8 miles, although we both ended up at exactly the same place.
Coordinate time is a property of places, proper time is a property of paths.
So the reason clocks physically get out of sync is that they are measuring the along-the-curve length of the path through spacetime, and people following different routes through spacetime will travel different distances. Clocks don't measure coordinate time (unless they move in a straight line along the coordinate axis), they measure proper time.
The analogy works quite well for a lot of purposes, but there is a big difference between Euclidean geometry and Minkowski geometry, which boils down to the form of Pythagoras's Theorem. In Euclidean space, the squared length of the hypotenuse of a right-angled triangle is the sum of the squared lengths of the sides. In 3D, this looks like $h^2=x^2+y^2+z^2$. We can rotate our $xyz$ coordinates any way we like, the length remains the same. When we add a time coordinate (coordinate time, not proper time), the sign flips. So we can define a length $h^2=t^2-x^2-y^2-z^2$ which is the proper time along the straight path between two points, or we can take the other convention and define $h^2=-t^2+x^2+y^2+z^2$ which is the proper length as measured by a ruler in relativity. Either way, the length remains the same in any orthonormal coordinate system. Apart from this sign-flip, time dilation and length contraction in Minkowski space are exactly analogous to the mixing of forwards/sideways directions in Euclidean space described above. They work the same way.
Thus, clocks getting out of sync is physically no stranger than people taking different routes to the same place walking different distances along the way. The time you experience is measured along the path you follow.
You are asking for a physical explanation of the relativity of simultaneity, but the simple fact is that simultaneity itself is not physical. Simultaneity is a matter of arbitrary convention, not a matter of physical fact. It is determined by humans, not by nature. Nature cares about causality, only humans care about simultaneity.
The most famous simultaneity convention is Einstein’s. He proposed adopting a simultaneity convention defined by setting the one way speed of light equal to $c$. When Einstein’s convention is applied to two different inertial reference frames it is determined that they disagree.
He explicitly identified his synchronization convention as a matter of definition. Later, Hans Reichenbach showed that other arbitrary synchronization conventions are also possible and that no physical experiment could choose between them. Reichenbach’s convention was further refined by Anderson.
Because the choice of synchronization convention is a matter of choice there simply is no valid answer to your question of how do they physically get out of sync. Getting out of sync is not physical.
Your question assumes that two clocks are out of synch as a result of one ticking more slowly than the other. That is not correct. In SR all good clocks tick at the same rate.
The change in synchronisation between reference frames is a consequence of the 4-dimensional geometry of spacetime. If you and I are stationary relative to each other, your time axis and mine both point in the same direction. However, if we move relative to each other, your t axis and mine no longer point in the same direction, but become tilted relative to each other. A plane of constant time for you is one at right angles to your time axis, and a plane of constant time for me is one at right angles to my time axis. Since our time axes point in different directions, a plane of constant time in your frame is a sloping slice through time in my frame, and vice versa. That means that all along a plane of constant time in my frame, the time is increasingly ahead or behind in yours, ie increasingly out of synch with time in mine.
I'm not sure what you'd consider a good answer to your question, but consider this question for a moment instead:
New Question: You and I buy identical new cars, with the odometers set to zero. I drive to the mall and back. You drive three times around the perimeter of the country and back. After we've both returned, we notice that our odometers show different numbers. How did they our odometers get out of synch?
If you are able to formulate an answer to the New Question that makes you happy, that's also the answer to your original question.
Edited to add: Both your original question and the New Question are special cases of this:
More General Question: Given two points in a metric space and two paths connecting those points, how can the two paths have different lengths?
In your original question, the metric space in question is spacetime, the first point is a traveler's departure from (say) earth, the second point is the traveler's return, and the two paths are the paths followed by the earth and the traveler. In the New Question, the metric space is the surface of the earth, the two points are both equal to the point where we begin and end our journeys, and the two paths are mine and yours. With that dictionary, you can translate any answer to the New Question into an answer to the original question (and vice versa).
Time runs slower when you move at some speed. And time runs slower if you enter a field of gravity.
For the clocks on a GPS satellite, there is a strong effect of them being slower because the satellite is moving at high speed, and a weaker effect of them running faster because they are further away from earths gravity. (Strong = dozens of microseconds per day).
Yes, it is physical. Under certain conditions, time as observed from the outside of your system runs faster or slower, but it is time itself that changes, not your clock.
Inside your system you can't detect the effect because anything that might detect it is also slower. There is nothing that affects clocks specifically. Everything is affected in the exact same way, and your clock looks perfectly fine to you. If you were at 99% of the speed of light, where the effect would be clearly visible (unlike dozens of microseconds per day, which you personally can't observe), you won't notice it because you are slowed down exactly like the clock.
This is a fundamental law. You can't really ask a "mechanical explanation" of this because this law defines the mechanics. There are no gears working behind this.
The deepest explanation you can get for this is the "geometry of spacetime" : The Minkowski metric defines an invariant distance for events on spacetime.
In the rest frame of a clock, the events of different ticks of the clock take place at the same place in space. The Minkowski distance between two ticks is (because $x_2=x_1$):
$$(t_2-t_1) ^2- (x_2-x_1) ^2= (t_2-t_1) ^2$$
In a frame where the clock is moving, the same ticks happen at two different point in space, i. e. $(x'_2-x'_1)$ is non-zero. The Minkowski distance is:
$$(t_2'-t_1') ^2- (x'_2-x_1') ^2$$
The two Minkowski distances must be equal. So: $$(t_2'-t'_1) ^2- (x'_2-x'_1) ^2=(t_2-t_1) ^2$$
From this, it follows that $(t_2'-t_1') >(t_2-t_1) $
I actually disagree with the comparatively universal contention in the answers so far that there isn't a "mechanical" or "physical" explanation for the slowing of a moving clock. Because there will be such an explanation depending on the precise mechanism of the clock. The actually surprising thing is that the dilatation ends up the same regardless of what actual mechanism the clock employs internally.
The simplest clock for looking at dilatation is a light clock that measures the time light takes to travel to a mirror in a fixed distance and back again. The equivalence of reference frames requires that the light in all reference frames travels at the same speed, but when a light clock moves sideways, the light has to travel at a zigzag path rather than straight back and forth and consequently takes a longer time when viewed from a non-moving frame.
Essentially all clocks work using some periodic process like the back-and-forth of light traveling to a mirror, and all periodic physical processes are delayed by the same amount when looking from outside of a moving frame, even if the "light clock" thought experiment, being tied into light propagation directly, is perhaps the easiest for working out the relations.
Though other properties that can determine oscillator frequencies, like length, electrical and magnetic fields, masses, and so on, all behave under movement in a manner that does not allow determining one physically preferred frame of reference.
So the whole ensemble of physical properties behaves in a uniform manner that can be represented by transforming the notion of time as the duration of repetitive mechanical processes in the same manner.
The answer is given previously are correct, but I don't think they explain what you are looking for. The answer is that one clock literally does tick slower than the other. So imagine that you are standing on the Earth with a clock next to you, ticking away. Another clock is on a rocket ship that is circling the earth right past you, at a very high speed, what we would call a relativistic speed. You would clearly see that time is passing slower, or that the clock on the rocket is ticking slower than your clock. If one minute passed on your clock, on the rocket clock perhaps only 59 seconds has passed as it passes by you. And each time that the rocket passed by the difference between your clocks would be greater and greater. So yes it is a physical actual slowing of time and thus a slowing of the ticking of the clock on the relativistic rocket. That is the physical meaning of special relativity. And keep in mind that it is not just a clock that changes but time itself, so the beating of the heart of the astronaut in the rocket and the aging of his cells all occur at the slowing rate
