What is the explanation of greater torque having greater "rotatory effect" on a stationary body?

Question

Why does moving a constant force further from center of mass (and thus increasing torque) increase angular acceleration? I know that the explanation for my question is that during the same angular displacement the same amount of force would be exerted over longer (linear) displacement, hence doing more work, and since conservation of energy is a thing the angular acceleration would increase, but it (at least for me) doesn't explain why moving a weight on a balanced beam makes it move (because when it is not yet moving, no work is being done and I can't mathematically prove that it would move).

Answer 1

I used to ask myself a similar question: How does a load at one end of a lever know how far away along the lever another force is being exerted? Forgive the anthropomorphic phrasing, but I hope you get my drift.

I solved my problem by realising that the lever had to have some internal structure. I considered the case of a lever of length 6$a$, pivoted at a point one third of the way along. I envisaged a lever in the form of a pin-jointed lattice of thin weightless struts and ties. The bottom of the lever is a thin horizontal rod of length 6$a$, resting on the pivot. A distance $a$ above the bottom rod is another thin horizontal rod. Between the two rods are 6 rods of length $\sqrt 2 a$, angled at 45°, each at 90° to its neighbour(s), to form a lattice running from one end of the bottom rod to the other. Two of the angled rods are one side of the pivot; the other four are on the other side; the top horizontal rod needs to be only $4a$ long.

You will find simply by applying force resolution at each joint that if a force $W$ is applied downwards at the end of the long arm of the lever, a force $2W$ is needed at the end of the short arm, in order to have equilibrium.

I then convinced myself that this result is independent of the particular internal structure chosen. This is almost certainly a very eccentric method of establishing the law of the lever (principle of moments) but I found it instructive and convincing!

Answer 2

You can experience this effect if you go to your local playground and use the seesaw. Ask a friend to sit at a fixed position, then sit down at different leverages. The seesaw will rotate.

This effect is not "due to conservation of energy". However, we can use "energy considerations" to calculate the point of equilibrium. This is motivated in the following picture:

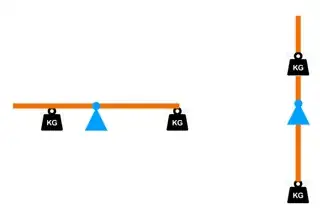
The left picture sketches the initial state and the right picture the equilibrium state.

Answer 3

Not sure this will address your concern, but here goes:

When the beam is stationary, the center of mass due to the weights on both sides is directly over the fulcrum and there is zero net torque as measured about the fulcrum. If one weight is moved, the c.m. shifts so it is no longer over the fulcrum. There is then a net torque about the fulcrum due to the weights, considered to be acting at the center of mass. The more the weight is moved, the more the c.m. is shifted away from the fulcrum therefore it has more effect so that's how the radius comes into play.

Answer 4

We can imagine a limit situation, where a mass $m$ is very far from the pivot point, that is when the distance $r \to \infty$. And the rod joining it to that point has a very small mass compared to $m$.

At a first approximation, the movement is linear for an observer close to $m$, and by the second Newton's Law: $\mathbf F = m\mathbf a$.

If we suppose the force orthogonal to the radius $r$: $$Fr = mar = mr^2\frac{a}{r} \implies \tau = I\alpha$$

Answer 5

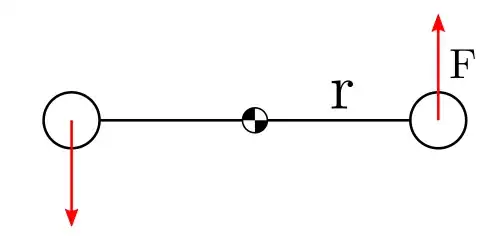
Does it though? Increasing the arm (for a constant force) always increases force, but the angular acceleration doesn't necessarily have to. Consider two point masses connected by a rod of length $2r$ (see figure below). To each point mass a force of strength $F$ is applied always at 90 degrees to the rod. I choose this setup to simplify the situation as much as possible.

In this case the angular acceleration can be found simply by \begin{align} \alpha&=\frac{\tau}{I}\\ &=\frac{2rF}{2mr^2}\\ &=\frac{F}{mr} \end{align} We find that, for constant force, the angular acceleration actually decreases! This makes sense if you imagine a very long and imagine how fast it rotates.

Answer 6

Maybe look at it the other way around -- in terms of work done.

The force involved comes from gravity.

When the two weights are balanced... if {the weight that we are going to move outwards (away from the fulcrum)} were to go down... the work done by gravity would be the same on the two weights, except that one would be negative.

If we move the weight away from the fulcrum -- say to 2 * {the original distance} -- then... if we imagine that it is moved down 1 unit of distance... the other weight is moved up 1/2 a unit of distance.

p.s. It feels tangentially relevant to say that... when doing calculations for, e.g. pushing down on a table, one imagines that the table is pushing back with equal force. This is strictly a fudge, to get the correct value for the equation, that results in the table not moving (up nor down).

Answer 7

Its already implied if we accept that a balanced beam wont rotate. Lets look at the case of an essentialy massless beam, and place the two equal weights $w$ a distance $d$ to the right and to the left of the fulcrum, respectively. Of course the beam wont rotate, otherwise it would mean that nature disobeys an almost trivial symmetry. If we then move the weights so they are both directly above the fulcrum, it still wont rotate, because of the same trivial symmetry. We deduce that a force acting directly through the fulcrum, wont cause the beam to rotate. Lets go back to the balanced beam with the weights a distance $d$ from the fulcrum. But now look at the situation with the left weight as the reference point. Seen from there, the normal force from the fulcrum is acting at a distance $d$ and with a force $2w$ upwards, and the rightmost weight is acting at a distance $2d$ with a force $w$ downwards. Now remove the fulcrum, but replace it with an equal force of magnitude $2w$ acting upwards, i.e. the same situation. Put the fulcrum directly under the leftmost weight, i.e. at the current reference point. The leftmost weight cant contribute, since its acting through the fulcrum (if you want, you can elongate the beam leftwards so that the beam is symmetric about the new fulcrumpoint, but that doesnt change anything as we consider the beam essentially massless). It follows that for nature to obey the trivial symmetry, it has to be the case that a force $2f$ at a distance $r$ from a point, must have the same tendency to rotate a beam as a force $f$ at a distance $2r$ from the point.