Can we use Ampere's law without requiring help from Biot-Savart law?

Question

Consider the case of a straight, infinite wire carrying uniform current. From reversing the direction of the current we can rule out radial dependence of the magnetic field but are left with two possibilities: a circumferential field and a longitudinal field. Can we proceed further from here without using Biot-Savart law and only applying Ampere's law?

Answer 1

Yes. Because Maxwell's Equations are an axiomatic theory of E&M, it must be true that one can use them without appealing to the "laws" that are derived from them. The key is to make a symmetry argument to determine the some properties of the unknown field, before using one of Maxwell's equations to calculate.

It is easiest to demonstrate the idea with Gauss's Law first. Just as Biot-Savart is often used to specify the direction of $\vec{B}$ when applying Ampere's Law in introductory physics, we similarly appeal to Coulomb's law to determine the direction of the unknown $\vec{E}$ field due to a given source. Then Gauss's law is used only to determine the magnitude $\left|\vec{E}\right|$. Let's instead solve this problem without using Coulomb's law.

Consider a spherically symmetric positively-charged object of uniform density. We make a symmetry argument:

A rotation of this object about any axis passing through its center, by any angle, leaves the object unchanged (because it is spherically symmetric). Therefore, the electric field that the charged object generates must also be unchanged by the same transformation (because the source has not changed). This has two consequences: (1) If we choose a point in space on the axis of rotation, we see that the electric field vector cannot point off axis (because if it did, its direction would be changed under rotation). Therefore, that electric field vector must point toward or away from the center of the source. For any point in space one can find such a symmetry axis passing through it, so all electric field vectors are radial. (2) A point in space that is off-axis, located a distance $d$ from the center of the source, will be mapped under the rotation to another point in space that also lies on the sphere of radius $d$. Therefore all electric field vectors on a sphere about the center of the source must have the same magnitude.

These two facts are required to determine $\vec{E}$ using Gauss's Law. Choosing the gaussian surface, $S$, to be a sphere of radius $r>R_{\rm source}$ about the charge center, we have \begin{align} \int_S \vec{E} \cdot \hat{n} \, {\rm d}A &= \frac{Q_{\text{enc by } S}}{\varepsilon_0} \\ \int_S \left|\vec{E}\left(\vec{r}\right)\right| \, {\rm d}A &= \frac{\rho V_{\rm source}}{\varepsilon_0} \\ \left| \vec{E}\left(r\right) \right| \, \int_S {\rm d}A &= \frac{q_{\rm source}}{\varepsilon_0} \\ \left| \vec{E}\left(r\right) \right| \, 4\pi r^2 &= \frac{q_{\rm source}}{\varepsilon_0}\\ & \rightarrow E(r) = \frac{1}{4 \pi \epsilon_0} \frac{q_{\rm source}}{r^2} \end{align} where fact (1) was used in going from line 1 to line 2 ($\vec{E}$ is parallel to the normal $\hat{n}$ of the spherical surface at every point on the surface), and fact (2) was used going from line 2 to line 3 ($E\left(\vec{r}\right)= E\left(r\right)$, i.e., the magnitude is the same at all points on the sphere, so it is a constant of the integral). There is one more subtle point about whether $\vec{E}$ points toward or away from the source charge: that will determine the sign of $\vec{E} \cdot \hat{n}$, which must agree with $q_{\rm source}$.

Now that we derived Coulomb's Law from Maxwell's Equations (without using Coulomb's Law to do so!), we could use it to construct electric fields of non-symmetric continuous charge distributions. But there are other symmetric charged objects (infinite cylinder, infinite plane) for which the above technique works directly.

For Ampere's law applied to the long straight wire, the method is exactly the same: use symmetry arguments to determine the facts needed to apply the law in the familiar way (using a circle for the "amperian loop"). There is a cylindrical rotational symmetry of the source, and a symmetry of reflection about a perpendicular plane plus a rotation by $\pi$ radians (since the source current direction is reversed by either of the two alone). There is one additional fact that must be taken into account, however: the magnetic field is a "pseudovector" rather than a vector, which means its direction reverses under a reflection transformation. Using that information you should be able to make a set of symmetry arguments that provide all of the information needed to perform the Ampere's law calculation without appealing to Biot-Savart.

Answer 2

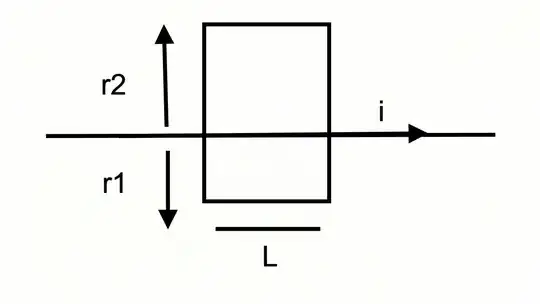
After posting this question I realized that we do not need Biot-Savart Law to rule out a longitudinal dependence. Construct a rectangular loop lying in a plane normal to the direction of the current, and let it be off-center, so that the upper segment is at $r_2$, while the lower is at $r_1$ with $r_2>r_1$ as shown.

Now, we have ruled out any radial directional dependence, and from symmetry, there should be no azimuthal dependence of magnitude. Also, due to the infinite extent of the wire, if $B_z$ exists, it must be a constant wrt to $z$ at most. Thus, based on these, we can propose

$$B_z\rightarrow B_z(r)$$

Now, apply Ampere's law to the loop shown, since there are no radial components of the field and no currents pass through the loop we get

$$\oint \vec B\cdot d\vec l=(B_z(r_2)-B_z(r_1))L=0 \\B_z(r_2)=B_z(r_1) $$

Since at $r_2\rightarrow\infty$ all fields should go to zero, we get $$B_z(\infty)- B_z(r_1)=0- B_z(r_1) =0$$

Thus, it shows that there is no $B_z$ component.

PS: comments below this post are in reference to my earlier incorrect answer and not the one written above