Why is a receiving antenna optimal at $\frac{\lambda}{2}$, mathematically?

Question

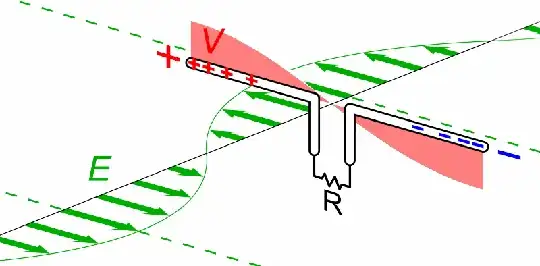
I can understand the qualitative argument of a recieving antenna becoming resonant: An external $E$-field causes the charges to move in a conductor and bunch up, creating a voltage. If the driving $E$-field's frequency is too high, the charges do not have enough time to seperate to the fullest. If the frequency is too low, it takes too long.

I am not convinced how the sweetspot of an antenna length of $L = \frac{\lambda}{2}$ arises mathematically, however.

In principle, only three equations should be needed to explain the system in one dimension and arrive at the supposed optimal length:

1. Ohm's law: $$j = \sigma E \;\;\;,$$ which causes the current in the conductor created by the external sinusoidal field.
2. The continuity equation: $$\partial_t \rho + \partial_x j = 0 \;\;\;,$$ which will then cause the charges to bunch up at the ends of the antenna (with the boundary condition $j=0$ at both ends).
3. Coulomb's law: $$E = \frac{1}{4 \pi \varepsilon_0} \int_L \frac{\rho(x') (x-x')}{|x-x'|^3}\text{d}x' \;\;\;,$$ by which the bunched up charges create a field opposing their accumulation at the ends.

How does one show that this system will be optimal if the antenna length is $L = \frac{\lambda}{2}$ of the driving $E$-field? What does optimal mean in this case? (Maximum charge accumulation at the ends?)

I have searched in electrodynamics textbooks and RF textbooks, but could never find a rigorous mathematical derivation.

Answer 1

You won't find a rigorous mathematical derivation because the relationship is approximate and practical.

Basically, the feed launches electromagnetic waves down the dipole legs. Near the wire, the field is similar to the field in a coaxial cable, and that resemblance dominates the dynamics. The waves propagate to the open-circuited ends, get reflected, and propagate back to the feed. You get resonance when the reflected wave at the feed is in phase with the wave coming in through the feedline.

You can analyze this with more rigor if you replace the wires with perfect coaxial lines of infinitesimal diameter, but, while such a construction resonates, it doesn't radiate.

Answer 2

The issue is basically the need to match the electrical impedance of free space to that of a split wire, as in a dipole. This minimizes power losses and reflections as the freely-propagating EM wave interacts with the wire to induce the flow of current through it. Mathematically, the matched impedance condition for the maximum possible power transfer occurs when the dipole wire length is 1/2 of a wavelength.

The derivation of this relationship can be found in any electrical engineering textbook dealing with antenna design.