1

So I am exploring my Cyr wheel (not me performing), and I want to try to express its movement in the best possible way. I will not be attempting the impossible, so just the wheel/ring/hoop, and not the wheel+human system.

Assuming no slipping and that the wheel is always in contact with the floor. Radius of ring is much bigger than thickness. (1 m and 1.5 cm)

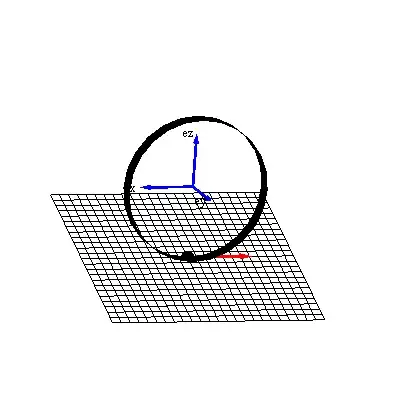
Defining the $xyz$ coordinate system with the $yz$ plane as the plane of the wheel, and the $x$-axis as the axis of symmetric rotation (rolling). We then also have a spinning motion about the z-axis, and a tilt/fall along the y-axis. Now, I know that this is where my mistake lies, because as the wheel tilts either the coordinate system will not follow the wheel (easiest to visualize) and so x is no longer the symmetric axis, or the coordinate system follows the wheel (maybe easiest to calculate?) and rotation about y loses meaning.

We have $$ T = \frac{1}{2}mv^2+\frac{1}{2}I_x\omega_x^2+\frac{1}{2}I_y\omega_y^2+\frac{1}{2}I_z\omega_z^2, $$ $$ V = mgh = mg\sin\phi, $$ with $\phi$ as the angle between the plane of the wheel and the floor. Since we have no slipping (or rather, no "travelling" slipping, as the wheel can still spin), $v=\omega_xr$.

$I_x=mr^2$, $I_y=I_z=\frac{1}{2}mr^2$, and defining $\omega_x = \dot{\theta}$, $\omega_y = \omega$, $\omega_x = \dot{\phi}$, gives $$ L = \frac{1}{2}mr^2\left(2\dot{\theta}^2+\frac{1}{2}\omega^2+\frac{1}{2}\dot{\phi}^2\right)-mgr\sin\phi, $$ yielding $$ \ddot{\phi} = 2g\cos\phi,\, \ddot{\theta}=0,\, \dot{\omega}=0. $$ The answers make sense in a naive way, but they provide no information about for example rolling at an angle in a circle or spinning or a combination of the two. Energy lost to friction shouldn't matter in order to produce some illuminating results, right?

I've already seen this question about a coin and this paper about a tilted rolling disk, but I'm afraid it's been too long since uni for me to be able to make the transfer. I'm also guessing there's quite a few similarities to an Euler disc. Any and all help appreciated!

Erikinho
  • 11
  • 3

1 Answers1

1

enter image description here

this animation is done with those equations of motion

\begin{align*} &\begin{bmatrix} \ddot{\varphi} \\\\ \ddot{\psi} \\\\ \ddot{\vartheta} \\\\ \ddot{x} \\\\ \ddot{y} \\\\ \ddot{z} \\\\ \end{bmatrix}= \left[ \begin {array}{c} -{\frac {mg\sin \left( \varphi \right) \cos \left( \vartheta \right) \rho}{{\rho}^{2}m+{ I_x}}} \\\\ {\frac {\sin \left( \varphi \right) mg\sin \left( \vartheta \right) \rho}{\cos \left( \varphi \right) \left( {\rho}^{2}m+{ I_x} \right) }}\\\\ -{\frac {mg\sin \left( \vartheta \right) \rho}{\cos \left( \varphi \right) \left( {\rho}^{2}m+{ I_x} \right) }}\\\\ -{\frac {mg\cos \left( \varphi \right) \sin \left( \vartheta \right) {\rho}^{2}}{{ \rho}^{2}m+{ I_x}}}\\\\ {\frac {{\rho}^{2}mg\sin \left( \varphi \right) }{{\rho}^{2}m+{ I_x}}}\\\\ 0 \end {array} \right] \end{align*}

enter image description here

where

  • $\varphi~$ rotation about the x axis
  • $\vartheta~$ rotation about the y axis
  • $\psi~$ rotation about the z axis
  • $x~,y~,z~$ center of mass position
  • $\rho~$ring radius
  • $I_x~$ inertia about the x axis

the position of the ring center of mass is a circular motion

enter image description here

with the kinetic energy and potential energy

$$ T=\frac{m}{2}\vec{v}^T\,\vec{v}+\frac{1}{2}\vec{\omega}^T\,\Theta\,\vec{\omega}\quad, U=-mg\cos \left( \varphi \right) \cos \left( \vartheta \right)\\ \vec\omega= \left[ \begin {array}{c} \cos \left( \vartheta \right) \dot\varphi - \cos \left( \varphi \right) \sin \left( \vartheta \right) \dot\psi \\ \sin \left( \varphi \right) \dot\psi +\dot\vartheta \\ \sin \left( \vartheta \right) \dot\varphi +\cos \left( \varphi \right) \cos \left( \vartheta \right) \dot\psi \end {array} \right]$$ the non-holonomic rolling conditions

$$e_{Nh}= \left[ \begin {array}{c} { \dot{x}}+ \left( \sin \left( \varphi \right) \dot\psi +\dot\vartheta \right) \rho\\ { \dot{y}}- \left( \cos \left( \vartheta \right) \dot\varphi -\cos \left( \varphi \right) \sin \left( \vartheta \right) \dot\psi \right) \rho \end {array} \right]=\vec 0 $$

and additional to keep the z coordinate of the center of mass constant ,the holonomic constraint equation $~z-\rho=0~$

you can obtain the EOM's

Eli
  • 13,829