Newton-Euler formulation

Question

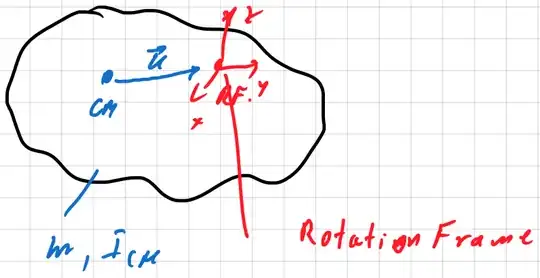
How to find the translational and rotational equations of motion when the center of gravity does not coincide with the origin of the fixed-body rotating frame?

Answer 1

The dynamical equations governing the translation and rotation of a rigid body are

$\dfrac{d \mathbf{Q}}{dt} = \mathbf{R}^{e}$
$\dfrac{d \mathbf{\Gamma}_H}{dt} = -\dot{\mathbf{x}}_H \times \mathbf{Q} + \mathbf{M}_H^{e}$,

being $\mathbf{Q}$ the momentum of the body, $\mathbf{R}^e$ the resultant of the external forces acting on the body, $H$ the pole w.r.t the angular momentum $\mathbf{\Gamma}_H$ and the moment $\mathbf{M}_H$ are expressed, $\mathbf{x}_H(t)$ is the position of the pole.

In these equations $H$ is an arbitrary geometrical point.

If you need to write the momentum and the angular momentum in terms of the angular velocity $\boldsymbol{\omega}$ and the velocity of a point $P$ that is not the center of mass, you can easily verify (using the rigid body motion) that

• $\mathbf{Q} = m \mathbf{v}_G = m \left[ \mathbf{v}_P + \boldsymbol\omega \times (\mathbf{r}_G - \mathbf{r}_P ) \right] = m \mathbf{v}_P - m (\mathbf{r}_G - \mathbf{r}_P )\times \omega = m \mathbf{v}_P + \mathbb{S}_P \cdot \boldsymbol\omega$;

• $\mathbf{\Gamma}_H = \displaystyle \int_V \rho (\mathbf{r} - \mathbf{r}_H) \times \mathbf{v} = \dots$ using the definition of the angular momentum you can express it w.r.t. the point you need; as an example, if you know the tensor of inertia w.r.t. the point $P$, we can write:

  $\mathbf{\Gamma}_H = \displaystyle \int_V \rho (\mathbf{r} - \mathbf{r}_H) \times \mathbf{v} = \displaystyle \int_V \rho [(\mathbf{r} - \mathbf{r}_P) + (\mathbf{r}_P - \mathbf{r}_H) ] \times [ \mathbf{v}_P + \boldsymbol\omega \times (\mathbf{r} - \mathbf{r}_P)]$

  and rewrite it as

  $\mathbf{\Gamma}_H = \displaystyle \int_V \rho (\mathbf{r} - \mathbf{r}_P) \times \mathbf{v}_P + (\mathbf{r}_P - \mathbf{r}_H) \times \int_V \rho \mathbf{v}_P - \int_V \rho (\mathbf{r} - \mathbf{r}_P) \times (\mathbf{r} - \mathbf{r}_P) \times \boldsymbol\omega - (\mathbf{r}_P - \mathbf{r}_H) \times \int_V \rho (\mathbf{r} - \mathbf{r}_P) \times \boldsymbol\omega =$
  $\qquad \quad = m(\mathbf{r}_G - \mathbf{r}_P) \times \mathbf{v}_P + (\mathbf{r}_P - \mathbf{r}_H) \times m \mathbf{v}_P + \mathbb{I}_P \cdot \boldsymbol\omega - (\mathbf{r}_P - \mathbf{r}_H) \times m (\mathbf{r}_G - \mathbf{r}_P) \times \boldsymbol\omega = \dots$ and so on

Answer 2

\begin{align*} & \textbf{Translation}\\ &m\,\vec{a}_{CM}=\vec{F}_{CM}+\vec{F}_P\\\\ &\vec{F}_P=-m\left[\vec{\omega}\times\left(\vec{\omega}\times\vec{r}_{CM}\right)+ 2\left(\vec{\omega}\times\vec{v}_{CM}\right)+ \vec{\dot{\omega}}\times\vec{r}_{CM}\right]\\\\ & \textbf{Rotation}\\ &\mathbf{ I}_P\vec{\dot{\omega}}=\vec{u}\times\left(\vec{F}_{CM}+\vec{F}_P\right)- \vec{\omega}\times\left(\mathbf{I}_P\,\vec{\omega}\right)+\vec\tau_{CM}\\ &\mathbf{I}_P=\mathbf{I}_{CM}+m\,\mathbf{U}^T\mathbf{U}\quad, \mathbf{U}= \left[ \begin {array}{ccc} 0&-u_{{z}}&u_{{y}}\\ u_{ {z}}&0&-u_{{x}}\\ -u_{{y}}&u_{{x}}&0\end {array} \right] \end{align*} \begin{align*} &\textbf{Translation plus Rotation}\\ &\begin{bmatrix} m\,E_3 & -m\,[\mathbf{r}_{CM}]^\times \\ 0 & \mathbf{I}_P-m\,[\mathbf{\vec{u}\times\vec r_{CM}}]^\times \\ \end{bmatrix} \begin{bmatrix} \vec{a}_{CM} \\ \vec{\dot{\omega}} \\ \end{bmatrix} =\begin{bmatrix} \vec{F}_{PR} \\ \vec{u}\times\left(\vec{F}_{CM}+\vec{F}_{PR}\right)- \vec{\omega}\times\left(\mathbf{I}_P\,\vec{\omega}\right)+\vec\tau_{CM} \\ \end{bmatrix}\\\\ &\vec{F}_{PR}=-m\left[\vec{\omega}\times\left(\vec{\omega}\times\vec{r}_{CM}\right)+ 2\left(\vec{\omega}\times\vec{v}_{CM}\right) \right] \end{align*}

• $~\vec F~$ forces
• $~\vec\tau~$ external torque
• $~\mathbf I~$ Inertia
• $~CM~$ center of mass
• $~P~$ pseudo

---

\begin{align*} &[\mathbf{\vec{u}\times\vec r_{CM}}]^\times= \begin{bmatrix} 0 & -z & y \\ z & 0 & -x \\ -y & x & 0 \\ \end{bmatrix}\quad, \text{where}\quad \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix}=\vec{u}\times\vec{r}_{CM}\\ \end{align*}

Notice

all vector components are given in the Rotation-Frame, thus the position vector of the center of mass in inertial system is:

$$\vec r_I(t)=\mathbf R(\varphi_i)\vec r_{CM}(t)$$

where $~\varphi_i=\varphi_i(t)~,i=1..3~$ are the Euler angles.

to get the result, you need additional three differential equations which are

with the rotation matrix $~\mathbf R(\varphi_i)~$ you obtain the angular velocity vector $~\vec\omega~$

$$\vec\omega=\mathbf J_R(\vec \varphi)\,\vec{\dot{\varphi}}\quad\Rightarrow\\ \vec{\dot{\varphi}}=[\mathbf{J}_R]^{-1}\,\vec\omega$$

all together you obtain 9 first order differential equations