DART crash on Dimorphos: computation of orbital period change

Question

What is the distribution of expected changes in the period of Dimorphos' orbit around Didymos when the spacevehicle DART crashes against it?

Answer 1

Here's a preliminary attempt to answer.

It assumes that the effect of the collision is purely elastic or inelastic giving a change in orbit time of 7.5 to 15 minutes. This is different from the observed 32 minutes. That difference is because this computation does not take into account that DART will form a crater and rock fragments from the crater will result in additional momentum and kinetic energy transferred to Dimorphos. Or potentially there will be comet like ejection of material.

Crash speeds

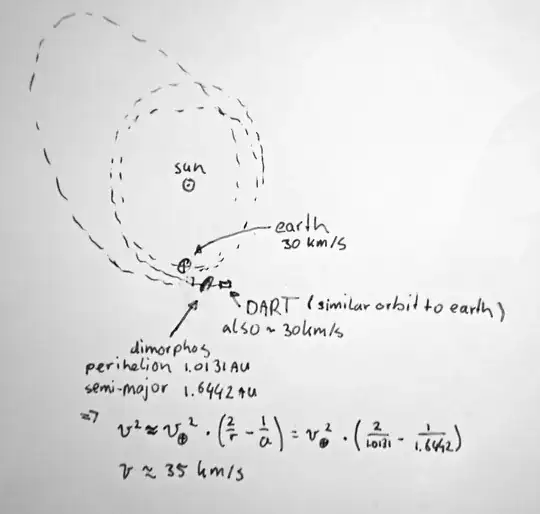
DART has an orbit similar to earth and we might approximate the speed as being equal to earth's speed relative to the sun: 30 km/s

Dimorphos gas an elliptical orbit and we can use the distance $r$ and semi-major axis $a$ along with the vis-viva equation to compute the speed.

$$v^2 = GM\left(\frac{2}{r} - \frac{1}{a}\right)$$

We get approximately 35 km/s.

So the relative speed will be 5 km/s.

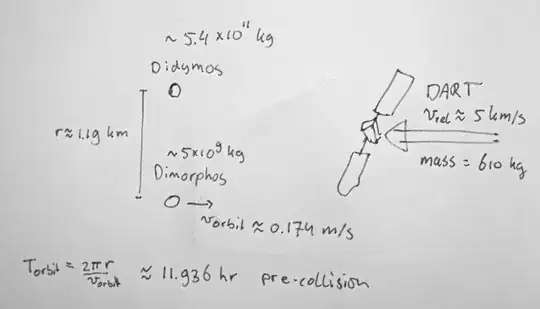
Masses

These we look up DART 610 kg, Dimorphos 5 x 10^9 kg, Didymos 5 x 10^11 kg

Period

The period of an orbit can be computed as

$$T = 2\pi \sqrt{\frac{a^3}{GM}}$$

where $a$ is the semi-major axis, $M$ the mass of Didymos (the effect of the mass od Dimorphos is negligible), and $G$ is the gravitational constant.

Velocity change

If the collision is inelastic and head on then we use

$$(0.174×5×10^9+5000×610)÷(5×10^9+610) \approx 0.17339$$

afterwards the orbital speed of Dimorphos is 0.17339 km/s instead of 0.174 km/s

Effect of velocity change on period.

We can express the period in terms of the semi-major axis, and the semi-major axis in terms of the velocity. So this allows us to express the period in terms of the velocity

$$a = \left(2/r - \frac{v^2}{GM}\right)^{-1} = \left(2\frac{v_{old}^2}{GM} - {\frac{v^2}{GM}}\right)^{-1} $$

where the second equality is based on assuming $a = r$ before impact.

Filling this into the equation for the period

$$T = 2\pi \mu^{-0.5}\left(2\frac{v_{old}^2}{GM} - {\frac{v^2}{GM}}\right)^{-1.5}$$

and the ratio will be

$$\frac{T_{new}}{T_{old}} = \left( 2- \frac{v^2}{v_{old}^2} \right)^{-1.5}$$

Which gives $T_{new} \approx 0.9896 \, T_{old}$ and the orbit period will be 447 seconds shorter for an inelastic collision (dimorphos moves slower but the orbit will be smaller making the orbit take less long).

For an elastic collision the change in speed will be approximately double and the change in the orbit time can be 894 seconds or approximately 15 minutes.

Answer 2

Here's my approach.

We set $ \mu = G(M+m) $ and use Keplers 3rd law

$$ T^2 = 4\pi^2 \frac{a^3}{\mu} $$

and the vis-a-vis equation

$$ \frac{v^2}{\mu} = \frac{2}{r} - \frac{1}{a} $$

With $r = a_0$ where ${}_0$ means "before impact" we find

$$ \frac{v_0^2}{\mu_0} = \frac{1}{a_0} $$

$$ \frac{v^2}{\mu} = \frac{2v_0^2}{\mu_0} - \frac{1}{a} $$

and therefore

$$ \frac{1}{a} = \frac{2v_0^2}{\mu_0} - \frac{v^2}{\mu} $$

Using Kepler's law to calculate

$$ \frac{T_0^2}{T^2} = \frac{\mu}{\mu_0} \frac{a_0^3}{a^3} = \frac{\mu}{\mu_0} \left(2 - \frac{\mu_0}{\mu} \frac{v^2}{v_0^2} \right)^3 $$

I find agreement with your result (but one could also take changes in mass into account *).

For collisions with small changes

$$ v_0 \to v + \Delta v; \; |\Delta v| \ll v $$

a first order Taylor expansion yields shorter (longer) orbital periods for decreased (increased) speed.

*) The approach does not address the calculation of the amount of ejected mass $\Delta m$ and its recoil i.e. the effect on $\Delta v$. However, it does address the secondary effect on the orbit once $\Delta m$ and $\Delta v$ are known. One can determine $\Delta T$ based on observations - NASA did that - and from that one could derive a range of allowed $\Delta m, \Delta v$. To nail it down exactly further models for the impact itself are necessary.