1

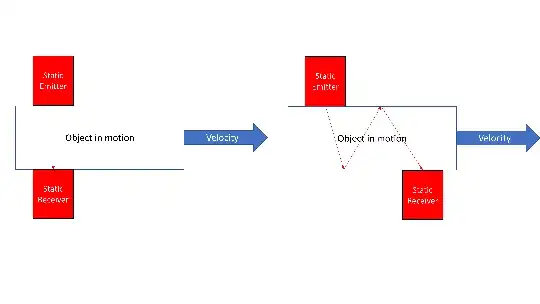
I am wondering if there would be any induced doppler-effects for a setup where a object is moving in a straight line but the emitting and receiving sensor are offset. The equation for the bistatic doppler shift is:

$f_D=2f*v/c_s*cos(\beta/2)cos(\delta)$

Where $f$ is the emitted frequency, $v,c_s$ are the velocity of the object and sound through the object, $\beta$ is the angle between the two sensors ($\pi$) and $\delta$ is the angle between $\beta/2$ and the direction the object is moving. Both the emitter and receiver would be completely stationary, they are not moving with the object. Essentially the object is sliding between the emitter and receiver which would be fixed to something else to prevent them from moving.

Using this equation I know for the left image that $\beta/2 = \pi/2$ will result in $cos(\pi/2)=0$, leading to no change ($f_D=0$) in the signal emitted.

What happens to the right image? Will it also have no change or is there another doppler-based (or something else) effect that would also change the signal as the object is in motion?

  • wavelength within medium 15 mm
  • medium thickness 3mm
  • Boundaries (reflection points in figure) moves together with the medium

enter image description here

iato
  • 145

1 Answers1

2

First off, your idea that a wave reflects at a boundary and forms some kind of "zigzag" within the medium doesn't work if the medium is much thinner than the wavelength. You must model the mechanics in a way that doesn't abstract to a level of "waves"; these can't form below a wavelength distance. It's a vibrating medium, not a medium in which waves propagate.

Also, ray-optics propagation wouldn't even happen if the medium was much thicker: Wavefronts aren't plane in such a slanted reflection, so the whole assumption that there's multiple discrete reflections won't work; you'd have to think of wave propagation in terms of solving wave equations under these small-scale boundary conditions, not just act as if waves were rays.

Anyway, none of this matters: your material boundaries, i.e., your reflection points, travel with the medium, and hence, are not subject to the Doppler effect. Regarding doppler, only the entry and exit from the moving medium matter. So, these pseudoreflections make no difference in your model.

As said, in reality, your (relative to wavelength) thin material necessitate that you understand the movement of your medium as less abstracted than "there's a wave with a wavelength in there", and short of finite element methods, I don't see how you'd precisely predict the waveform at the receiver; what is sure is that you'll have very different interference patterns at different shifts of the receiver; something really not represented by your model at all.

Marcus Müller
  • 277