1

My question is very similar to this one: Why is the field inside a hollow sphere zero?, but it's generalized to a non-spheric conductor, since we know that electrostatic field in the empty space (I'm not referring to the middle of the conductor, that's clear to me) of a hollow conductor is zero irrespective of the shape of the conductor. Could you show me why (even intuitively)?

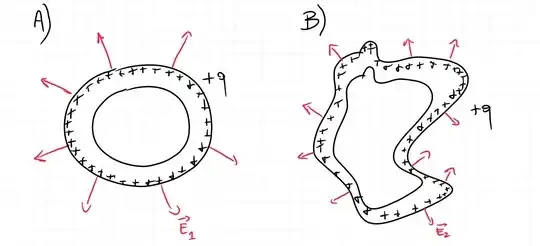
EDIT: I try to be more specific. We have the 2 situations in the image (no charge inside). In case A) the geometric reason why the electrostatic field in the hollow is zero is described in the thread I quoted before, but that explanation is true only for spheric conductors. Nevertheless, we know that the field in the hollow is zero irrespective to the shape of the conductor so it has to be zero in case B) too. How do you explain that by vectorial sum? My intuitive hypothesis is that the irregular shape produces not uniform (according to different radii of curvature) charge distribution on the surface and this two effects (irregular shape and irregular distribution) balance each other in order to cancel internal field in every point as the sphere does. Is that true? image

max
  • 11

6 Answers6

2

As FlatterMann says, you must assume there are no charges inside. You also must assume static conditions (no electromagnetic waves). The conductor is necessarily at constant potential, since if it isn't, it's not static: the potential difference will drive a flow of current through the conductor. There is thus no difference in potential between any part of the interior and any other part. With no potential difference, you have no field.

John Doty
  • 22,119
0

Suppose first of all that the conductor were solid. Under electrostatic equilibrium, there will be no field in the interior of the conductor because if there were any field, it would make charge carriers inside the conductors move around until there is no net field.

From the fact that $E = 0$ in the interior of the conductor, we also deduce that $\rho = \nabla \cdot E = 0$ in the interior. That means that even if the conductor carries any net charge, that charge must all go to the surface. Similarly, if there is any static external field, it will be cancelled in the interior of the conductor solely by induced charge on the surface.

Now, just remove the material from the interior. I don't mean reach in and remove it physically; I just mean that since this configuration with all charges on the surface satisfies Maxwell's equations, the same will be true of a hypothetical alternative configuration where the material in the interior of the conductor (which, recall, has zero charge density) is replaced by neutral air. Here the electric field will also be zero because the air has the same charge density as the material that it replaced (namely zero).

(As others have pointed out, if there are any charges in the interior of the hollow conductor, the field inside the conductor will not be zero.)

Brian Bi
  • 6,885
0

I think gauss law may have a good explanation to you, this law states that flux(Electric field passing through unit area) is equal to total charge enclosed within surface over epsilon not where epsilon not is the permativity of free space,also now matter how much charge you give to the conductor the extra charge always remains upon the outer surface of conductor never inside, since the charge enclosed by inner surface is zero so is the flux, now if the flux is zero it could mean that maybe electric field and area vector(vector perpendicular to area) are perpendicular to each other or the electric field is zero. Now you can clear the area vector being perpendicular to electric field since this conductor is subjectedemphasized text to its own field not external

This figure shows area vector enter image description here

Now the cylendrical figure you see is placed within external electric field so you can see that field lines are perependicular to some of the surface of cylinder like curved surface, but in the sphere problem the surface is experiencing its own electric field which can be never perpendicular

Maanik Khurana
  • 51
0

You can think of metal as a material of $\infty$ dielectric constant.

Now, $\vec{E}_d=\vec{E}\left(1-\frac{1}{k}\right)$, where $E_d$ is the opposing field dielectric produces(using induced bound charges) in response to the external electric field $E$. Such that the overall field inside the dielectric$=\vec{E}-\vec{E}_d$.

For metals, $k=\infty$. $\Rightarrow \vec{E}_d=\vec{E}$, so field inside the bulk of the material = $\vec{E}-\vec{E}_d=\vec{0}$.

0

The potential is constant at every point on the internal surface $S$ of the metal: $\phi(r\in S)=\phi_0$. Since there are no charges in the cavity, the potential $\phi(r)$ satisfies Laplace's equation $$\Delta \phi(r)=0$$

The solution $\phi(r)=\phi_0$ solves the equation with boundary condition $\phi(r\in S)=\phi_0$. Since the solution of Laplace equation with closed boundary must be unique (How do I show that the Laplace equation has a unique solution under the Dirichlet closed-surface boundary condition?), is the only solution and $\vec{E}=-\nabla \phi=0$ everywhere inside.

John
  • 4,287
0

It’s because of the uniqueness theorem of PDE. Since the potential distribution $V$ inside the hollow satisfying the Poisson equation with vanishing source term and the boundary conditions state that on the inner surface of the hollowed conductor, the potential is a constant, say $V_0$ and the partial derivatives of the potential (i.e. electric field) is zero. So one obvious solution satisfying this boundary condition and Poisson equation is that $V=V_0$ at all points inside the hollow. There is no other solutions due to the uniqueness theorem.

Tan
  • 1