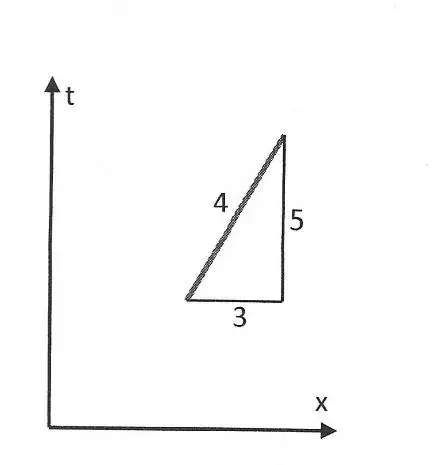
Spacetime manifolds, as well as their simplified form, twodimensional spacetime diagrams, are always Lorentzian (Lorentzian metric $ds^2 = dt^2 - dx^2$). Normally, the Lorentzian metric is hidden because spacetime is represented on a Euclidean support such as a sheet of paper, and we can measure the corresponding Euclidean distance ($ds^2 = dt^2 + dx^2$) even though it is completely meaningless. For instance, the Lorentzian metric in the diagram is $4$, but the measurement of the worldline yields the meaningless distance of $5.83$.
Is there a way to get rid of this superfluous Euclidean metric of the support of observation (such as a sheet of paper), or is the Euclidean metric a necessary accessory of the Lorentzian spacetime manifold?