I know this sounds elementary; that is why it has taken me this long to ask this question.
I understand how forces can be added this way (above).
But I don't see how it can be added in this way (second picture). Why is the resultant force (vector) equivalent to the line between those two forces (vector a and vector b) ?
It is self-evident that successive displacements add by the tail-to-head arrow method. Velocities, being rates of change of displacement, add in the same way, as must momenta, and therefore forces, being rates of change of momentum.
This is a hand-waving 'justification', but it worked for me as a better alternative to the parallelogram rule which, as a high school student, I had been presented with as if it were almost self-evident – but which seemed to me quite arbitrary.
Addendum: One has to realise, of course, that with the tail-to-head arrow method, the positions of the arrow-tails have nothing to do with the point(s) in space at which the forces act. The diagram performs a mathematical operation that could equally well be carried out on a calculator on the moon.
Here is one way of looking at it that might help you. To add vector A to vector B in the diagrams you provided, take each vector and draw its horizontal and vertical component like in this image.
It actually doesn't matter which directions you take as horizontal and vertical, so do whatever is most convenient (as long as your are consistent for both vector A and B).
Then add the vertical components of vectors A and B. They are pointing in the same direction, so this is what you said you are comfortable with. Do the same for the horizontal components. Now you have the vertical and horizontal components of the resultant vector, and you can draw the resultant vector itself.
Mathematically:
$\vec{A} + \vec{B} = \begin{pmatrix} A_x \\ A_y\end{pmatrix} + \begin{pmatrix} B_x \\ B_y\end{pmatrix} = \begin{pmatrix} A_x + B_x \\ A_y + B_y\end{pmatrix} $
This shows to add two vectors, you add their components in each dimension. Which is what you are comfortable with. Using triangles (or parallelograms) are useful and ultimately equivalent alternatives.
The idea of vectors addition, subtraction, resolution, etc. is found everywhere in life. Using basic trigonometry, one could show that some force $F$ that makes an angle $\theta$ with the horizontal would be equivalent to two forces. One force equal to $F\sin(\theta)$ in the y-direction and $F\cos(\theta)$ in the x-direction. This is reversible, which leads to the idea of vector additions and subtraction in diagrams (i.e. the tail-to-head method).
Hope that helps!
You are right that this is a non-trivial fact about forces, and it can only be justified by appealing to experiment. There is some discussion of this in Chapter 7 of Spivak's Physics for Mathematicians, where Spivak points to some purported proofs of the parallelogram rule and describes their limitations. As far as I know, the only justification for the parallelogram rule is that it is an assumption of Newton's laws (one that we nowadays treat as completely obvious, but that Newton was aware was not at all obvious, and which he attempted to prove independently of the other laws). We can therefore appeal to the tremendous empirical successes of Newton's laws and use the parallelogram rule without concern.
Just vector algebra. Force are vector physical quantities. You can sum them. When you sum them, you need to apply vector sum
Consider the forces acting consecutively on an object of unit mass. There is a push (acceleration) and then another push. Assume a coordinate system with its y-axis aligned with the first push such that $v_y =0$ at $y=0$ and $v_y =1$ at $y=1$. Assume the second push is along the x-axis with $v_x =0$ at $x=0$ and $v_x=1$ at $x=1$. The total acceleration must be given by $(1,1)$. If, instead, the force in the x direction brings the object to velocity 10 then the acceleration vector would be $(10,1)$. You said that you understand addition of forces along the same direction. So, that's it. Forces add like vectors.
It may help if you consider forces as infinitesimal momentum changes. I was recently convinced (also read the comments) that they are equivalent: $\vec F = d\vec p/dt.$
This may help because momentum is, for a given mass, just velocity; it is much more intuitive that velocity is a vector and can be added that way. For example, one can have a platform moving at constant velocity, and on that platform a vehicle moving in a different direction: It is clear that the resulting velocity relative to a "resting" observer is the addition of the two velocity vectors.1 Any change to the momentum vector — equivalent to a force — is, obviously, a vector as well.
Thinking about it, it is possible to experimentally (and intuitively) show that forces are also vectors which can be added as such, e.g. with two springs pulling at an angle at the same object, which will then be accelerated according to the vector-addition of the two forces. And, of course, the change in momentum is, as we said, equivalent to the acting force anyway :-) — it is the force.
1 Nobody except Einstein would think it could be anything else.
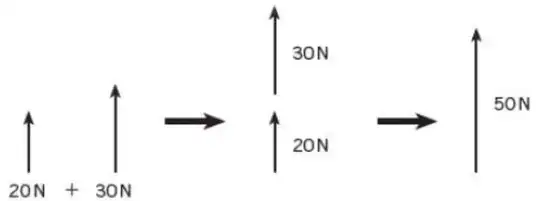
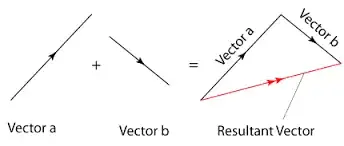
There is a simple answer. Forces add this way because they are vectors, and vectors add this way. It's just how their math works.
Of course, this is a bit of a cop-out. It's not quite satisfying because it starts from the assumption that forces are vectors. If they are vectors, it is easy to show they add this way, because they do. But why can we assume forces are vectors in the first place?
If we look at the mathematics, vectors have the following properties:
These are the properties of vector spaces. They're just a set of properties that showed up often enough in mathematics that we gave it a name and studied them a bit. That's all.
So the question for us is "do we believe" that forces have all of these properties? We can go down the list and convince ourselves that they do. For example, the first one (the associative property) can be shown that if Alice joins Bob and Charlie in pushing on an object, the forces they exert are the same as if Alice and Bob join Charlie. The difference between those two is so small that we intuitively might not even realize they're different. The fact that those situations are equivalent lets us know that forces follow this associative property.
Likewise we can find that it doesn't matter if we consider the force by Alice first, then Bob, or if we consider the force by Bob and then consider Alice, the result doesn't change. That's why it is commutative.
Its reasonably easy to think through the zero force and the idea that every force can have an inverse. In fact, we see that inverse quite often in the concept of "an equal and opposite reaction."
Multiplying by scalars is pretty easy to work through too. If Alice and Bob are applying forces, and then they apply 5x as much force, that is identical to Alice applying 5x more force and Bob applying 5x more force (again, so natural that one might not even realize those are different). And we can see that if Alice applies 2+5 pounds of force to something, that is equivalent to Alice applying 2 pounds and Bob applying 5 pounds in the same direction as Alice.
If you accept all of these things as true statements about forces, then you can conclude that forces are indeed vectors. And after concluding that, you can use all of the imagery we see in this question/answer to handle addition of vectors, such as the parallelogram image. Why do they add this way? If you sit down and hammer on the math long enough, you will realize that that is the only way two vectors could add which satisfies the above 7 properties. Any other addition will cause one of them to break down.
So that's really how forces can be added. You determine that forces have the properties of vectors, and then you know they must add in the only possible way vectors can add.
Probably the most important part of this addition approach is that addition of vectors is commutative. $a + b = b + a$. In most visualizations, you will notice that there are two paths you can take through the addition. One starts with $a$ and adds $b$ to it. The other starts with $b$ and adds $a$ to it. By the rules of vectors, those additions must commute, meaning they must give you the same value. You are free to try to find another way to add vectors, but most of the intuitive ones you may think of will not have this important property.
It is a question of an equivalence relation: equipollence.
https://math.stackexchange.com/questions/3350499/equipollent-couple-of-points-to-define-vectors
