0

I placed 250 evenly spaced identical positive charges Q=0.01 each (ignoring coulombs constant) around a hollow unit circle in mathematica and calculated the electric vector field:

m = CirclePoints[250];
f[p_] := 0.01*((x-p[[1]])/(((x-p[[1]])^2+(y-p[[2]])^2)^(3/2)));
g[p_] := 0.01*((y-p[[2]])/(((x-p[[1]])^2+(y-p[[2]])^2)^(3/2)));
VectorPlot[{Total[Map[f, m]], Total[Map[g, m]]} , {x, -2, 2}, {y, -2,2}, VectorColorFunction -> (ColorData["Rainbow"][#5]&) , PlotLegends -> BarLegend["Rainbow"], VectorColorFunctionScaling -> False, VectorRange -> All, VectorPoints -> 100]

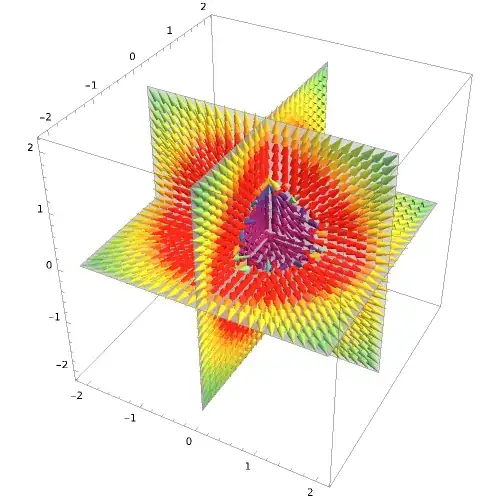
enter image description here

There is clearly still a field inside the circle, what am I missing?

Lewis Kelsey
  • 217

1 Answers1

0

By using inverse square with 3D as suggested, we get the following:

$$\sum_{p\in P} \left<\frac{x-p_x} {\sqrt{(x-p_x)^2 + (y-p_y)^2 + (z-p_z)^2} ^3} , \frac{y-p_y} {\sqrt{(x-p_x)^2 + (y-p_y)^2 + (z-p_z)^2} ^3}, \frac{z-p_z} {\sqrt{(x-p_x)^2 + (y-p_y)^2 + (z-p_z)^2}^3}\right>$$

m = SpherePoints[250];
f[p_] := 0.01*((x-p[[1]])/(((x-p[[1]])^2+(y-p[[2]])^2 + (z-p[[3]])^2)^(3/2)));
g[p_] := 0.01*((y-p[[2]])/(((x-p[[1]])^2+(y-p[[2]])^2 + (z-p[[3]])^2)^(3/2)));
h[p_] := 0.01*((z-p[[3]])/(((x-p[[1]])^2+(y-p[[2]])^2 + (z-p[[3]])^2)^(3/2)));
SliceVectorPlot3D[{Total[Map[f, m]], Total[Map[g, m]], Total[Map[h, m]]}, "CenterPlanes", {x, -2, 2}, {y, -2,2}, {z, - 2,2}, VectorColorFunction -> (ColorData["Rainbow"][#7]&) , PlotLegends -> BarLegend["Rainbow"], VectorColorFunctionScaling -> False, VectorRange -> All, VectorPoints -> 25, ImageSize -> {500,500}]

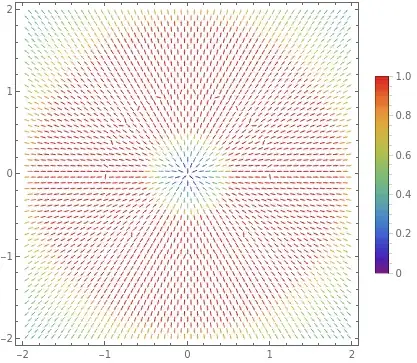
enter image description here

With 2D it requires reverse linear to get the expected result of no field inside the circle:

$$\sum_{p\in P} \left<\frac{x-p_x} {(x-p_x)^2 + (y-p_y)^2} , \frac{y-p_y} {(x-p_x)^2 + (y-p_y)^2}\right>$$

m = CirclePoints [125];
f[p_] := 0.01*((x-p[[1]])/(((x-p[[1]])^2+(y-p[[2]])^2)^(2/2)));
g[p_] := 0.01*((y-p[[2]])/(((x-p[[1]])^2+(y-p[[2]])^2)^(2/2)));
VectorPlot[{Total[Map[f, m]], Total[Map[g, m]]} , {x, -2, 2}, {y, -2,2}, VectorColorFunction -> (ColorData["Rainbow"][#5]&) , PlotLegends -> BarLegend["Rainbow"], VectorColorFunctionScaling -> False, VectorRange -> All, VectorPoints -> 50, ImageSize -> {500,500}]

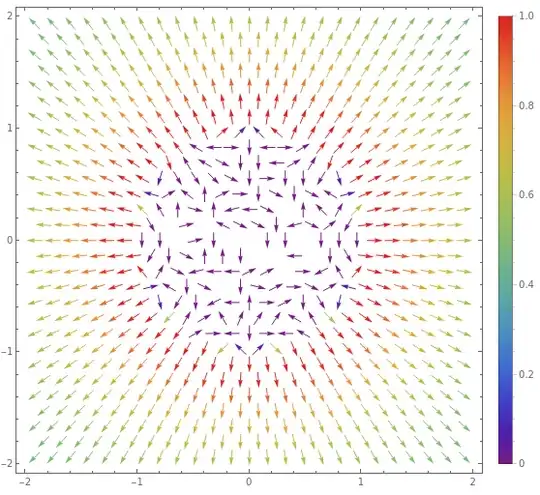
enter image description here

Red in these plots means anything over 1. The first equation looks like inverse cube but it's actually inverse square because you need to normalise the vector first, which involves another division by r.

Lewis Kelsey
  • 217