Particle horizon in an empty universe

Question

So in this thread, Can space expand with unlimited speed?, the author Pulsar made amazing diagrams of different horizons and paths for a benchmark model that describes our current universe, and gave a great explanation of how to interpret the diagram. Does someone have a version of the diagram for an empty and negatively curved universe? I'm trying to visualize what happens in that universe, and it seems the particle horizon at our age today 13.7 Gyr would be infinite, and I'm not sure how to interpret this result.

Answer 1

I'll assume that empty and negatively curved means $k<0$ and $ρ=p=Λ=0$.

In that case the Friedmann equations reduce to $\dot a = \pm\sqrt{-k}$ and $\ddot a=0$. The solutions are $a(t)=\pm\sqrt{-k}\,(t-t_0)$. I'll take $t_0=0$, and I'll assume you picked the positive-slope solution, $a(t)=t\sqrt{-k}$, since that has a "big bang" at a finite time in the past.

I put "big bang" in scare quotes because it is actually just a coordinate singularity. You can analytically extend the spacetime beyond it, and when you do, you get Minkowski space.

This diagram, which I adapted from this blog post, shows the relationship between FLRW and polar inertial coordinates.

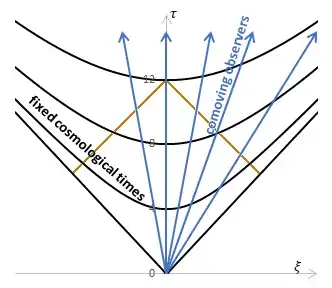
$ξ$ and $τ$ are the inertial coordinates, and the metric is $ds^2=dτ^2-dξ^2-ξ^2dΩ^2$, where $dΩ^2=dθ^2+\sin^2 θ\,d\phi^2$ – just standard polar coordinates for Minkowski space. The $θ$ and $\phi$ coordinates are shared between the Minkowski and FLRW coordinate systems, and are suppressed as usual. The Minkowski $(ξ,τ)$ and FLRW $(r,t)$ are related by

$$t = \sqrt{τ^2-ξ^2}, \qquad r = \frac{1}{\sqrt{-k}} \tanh^{-1}\,\frac{ξ}{τ}$$

The black curves are surfaces of constant FLRW time, and the blue lines are lines of constant FLRW position, or the worldlines of test particles moving with the Hubble flow (though there is really no Hubble flow in this cosmology, since the universe is empty).

The brown lines show the past light cone of a point at cosmological time $12$. You can see that it crosses all of the blue lines, and even if you added infinitely many more blue lines at evenly spaced rapidities, it would still cross all of them before hitting cosmological time $0$. That's why the particle horizon works out to be infinitely large.