Question regarding Group and Phase Velocity

Question

https://youtu.be/EIqKG5TiSYs.

I have some confusions regrading Group and Phase Velocity. Group Velocity exists for a group of waves, it's stated here in the video that Group Velocity the sum of the phase velocity of individual waves (Phase velocity is given by $\dfrac{ω}{k}$). If the Group velocity $\dfrac{dω}{dk}$is the sum of the phase Velocity of individual waves then why is it a differential quantity and not an integral quantity?

Answer 1

Your confusion is normal: phase and group velocity are the most poorly taught topics in physics.

Classical wave physics courses start with a plane wave:

$$ \psi (x,t)=U_{m}e^{i(k.x-\omega t)} $$

The plane wave extents from $x=- \infty $ to $x= \infty $ and oscillate in time from $t=- \infty $ to $t= \infty $.

In mechanics, the velocity of a point is precisely defined, but how do you define the velocity of a time changing curve whose domain is infinite?

The work around is usually done by introducing the phase of the plane wave:

$$ \phi (x,t)=k.x-\omega t $$

You could naively think the phase velocity is just the rate of change of the phase and calculate:

$$ \frac{d \phi (x,t)}{dt} = \frac{\partial \phi (x,t) }{\partial x}~ \frac{dx}{dt}+ \frac{\partial \phi (x,t)}{\partial t}=k\frac{dx}{dt}- \omega $$

But x and t are two independent variables. So $\frac{dx}{dt}=0$ and you get:

$$ \frac{d \phi (x,t)}{dt} = - \omega $$

Which is not the phase velocity people are talking about.

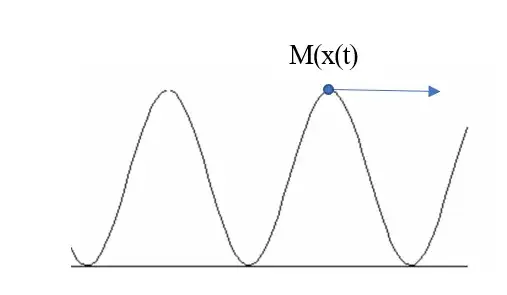
To get the good formula, you need to ask yourself what would be the velocity of a point M(x(t)) moving with the wave. The mental picture goes as follow. Imagine a surfer standing on the wave, its position at time t is x(t), and height of the wave is:

$$ \psi (x(t),t)=U_{m}~e^{i(k.x(t)-\omega t)}$$

As the surfer moves with the wave, he stays at the same height if the phase $k.x(t)-\omega t$ remains unchanged.

The phase velocity of a plane wave is thus the velocity of a point chosen on the envelope moving with the wave. Since $v_{\phi}=\frac{\omega}{k}$ does not depend on x(t), the phase velocity is independent of the chosen point and our definition makes sense.

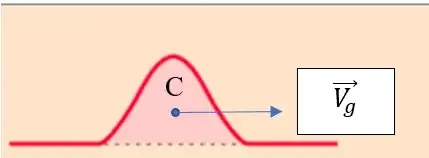
Plane waves infinite extension in both space and time makes them unsuitable to model real waves. If we consider a more general signal $\psi(x,t)$ (red curve), we are back to the starting point concerning the definition of the signal velocity. How do you define the velocity of something whose shape changes both in time and space?

We can no longer chose a random point on the envelope and say that its velocity is the wave velocity. Such a choice would lead to a wave velocity that differs with the chosen point. Our choice of M must be guided by simplicity and universality. The simplest choice that summarizes the whole curve is the centroid (center of gravity) of $\psi(x,t)$. Its position $x_{c}(t)$ is given by:

$$x_{c}(t)= \frac{ \int_ {-\infty }^{ \infty} x ~\psi(x,t)~ dx }{\int_ {-\infty }^{ \infty} \psi(x,t) ~dx }$$

It can be shown that the velocity of the centroid is the group velocity:

$$ V_{g}= \big( \frac{d~ \omega (k)}{dk} \big)_{k_{0}} $$

Some Explanations of the paper

We shall need some results about Fourier transform. The Fourier transform of $f(x)$ is $\hat{f} (k)$ defined by:

$$\hat{f} (k)= \int_{- \infty }^{ \infty } f(x) e^{- i k.x}dx ~~\rightleftharpoons ~~f(x)= \frac{1}{2 \pi } \int_{- \infty }^{ \infty } \hat{f}(k)e^{i k.x}dk$$

Using this definition, we find: $$\hat{f}(0)= \int_{- \infty }^{ \infty } f(x) dx $$

and: $$ \frac{d\hat{f}(k)}{dk}= - i \int_{- \infty }^{ \infty }x ~f(x) e^{- i k.x}dx ~~\Longrightarrow ~~\big(\frac{d\hat{f}(k)}{dk}\big)(0)= - i \int_{- \infty }^{ \infty }x ~f(x) dx $$

Plugin these two results into the definition of the centroid, it comes:

$$x_{c}(t)= \frac{ \int_ {-\infty }^{ \infty} x ~\psi(x,t)~ dx }{\int_ {-\infty }^{ \infty} \psi(x,t) ~dx }= -i \frac{ \big(\frac{ \partial \hat{\psi}(k,t) }{\partial k}\big)(0,t) }{\hat{\psi}(0,t)} $$

The centroid is thus related to the first two terms of the Taylor expansion of the Fourier's transform.

If you do not have access to the paper, below are the screenshots.

Answer 2

Group velocity isn't the sum of phase velocities, it's very easy to find reasons showing that it doesn't make any sense:

• Any real wave is the sum of an infinite number of harmonic waves, making that hypothetical sum dubious.
• For any electromagnetic wave in the unlimlited void, both its harmonic components and the complete wave travel at the same velocity $c$, so there's no addition.
• Velocities are not additive, this is not classical mechanics.
• Both velocities can even have opposite signs for the same wave, or one can be zero and not the other, and so on (depending on the medium).

In most cases, group velocity boils down to the velocity of the maximum of the wave packet, and can be different from the velocity of a local maximum of the wave. You'll find a few interesting animations on Wikipedia's page on group velocity.