Given that $\pi$ is the irrational number that occurs with a perfect circle, and perfection is very difficult to achieve through chance or nature, I think that most circles are really ovals, and imperfect.
Are there any proven naturally occurring objects, behaviors, movements, that have been so highly correlated with the irrational number $\pi$, that it can be assumed the underlying property is also a perfect circle?
Perfection is to be found in mathematics, not in our universe.
Having said this, if you are looking for an observable near-perfect realization of the transcendental number $\pi$ in nature, I would suggest not going for a circle, but rather for a sphere. A big sphere. In fact the largest sphere currently observable: the cosmic microwave background.
The cosmic microwave background radiation is the relic of the big bang that reaches us as a uniform thermal radiation coming from all directions in the sky. In each direction, the distance to the source is determined by the Hubble redshift. As, after subtraction from the Doppler shift due to our own motion, the radiation is observed to be isotropic to roughly one part in 100,000, we are talking about a sphere that is pretty perfect.
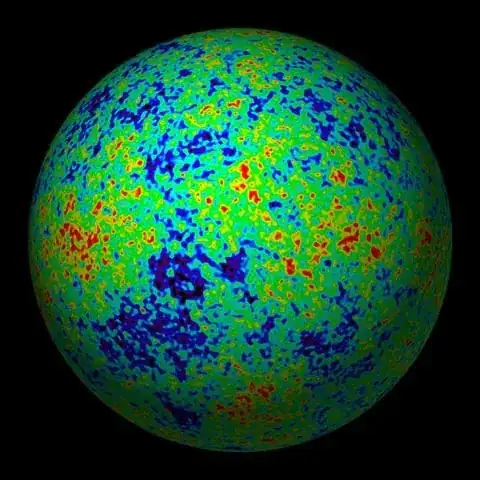
Or at least so the eyes of physicists who consider a cow to be spherical in good approximation...
Another occurrence of a close-to-ideal sphere is provided by the horizon of a stationary non-rotating black hole. But we have not (yet) observed such a horizon directly.
I do not know about perfect but naturally occurring yes:
The circles, according to [Norbert Juergens], are water traps created by a sand termite. The termites eat all the grass within a circular patch, exposing underlying sand grains that store any falling rainwater. These barren freckles are works of ecological engineering,
Then there are pearls:
In fact, scientists have recently confirmed the suspicions of pearl farmers who have long believed pearls with rotational symmetry really are "turned" – that is, they rotate as they grow within the pouch that holds them inside the soft mantle tissue of molluscs. A 2005 report published in the French language Journal des Perliculteurs states that they typically rotate once every 20 days or so. This would explain the rotational symmetry: any differences in growth rate along the axis or rotation get copied around the entire circumference.
If you were very rich and made a perfect cut of a completely spherical pearl it should be a perfect circle.
