Should the empirical Newton's gravitational constant $G$ be considered as the independent fundamental physical constant?

Question

It is known that the effect of gravitational waves generation in collisions of (black holes)/(neutron stars) pair follows from the predicted consequences of Einstein's General Theory of Relativity.

Newton's empirical gravitational constant $G$ is used in the analysis of captured gravitational waves produced by the collision of (black holes)/(neutron stars) pair.

Particularly I've heard that Newton's gravitational constant is used in calculations of masses of colliding (black holes)/(neutron stars) pair.

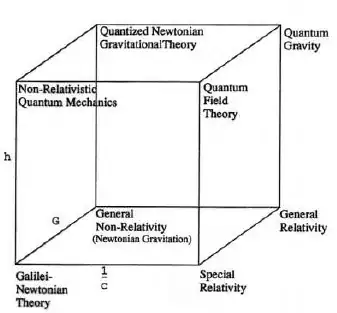
If so, this is an interesting (and even paradoxical) situation, when the two different theories of gravitation (the empirical Newton's and highly theoretical Einstein's) are used together.

I was pointed in PM 2Ring comment (see below) that the Einstein gravitational constant contains $G$.

So should Newton's empirical gravitational constant $G$ be considered as the independent fundamental physical constant, say on the par with the Speed of Light?

Another part of the paradox is that the numerical value of the Newton's gravitational constant is known per most current measurements with some certainty only to four significant digits - in SI units it is approximately $6.674×10^{−11} \,m^3 kg^{−1} s^{−2}$, while on another hand, the analysis of captured by LIGO/VIRGO gravitational waves is described as being done with quite high Bayesian precision.

Also see Gravitational Constant in Newtonian Gravity vs. General Relativity and links therein.

Answer 1

$G$ is considered a fundamental constant per current physics. Although it may have been empirical in Newton's law, all fundamental constants are empirical. One cannot derive $G$, $c$, $h$, or the ratio of proton to electron mass (for instance), from first principles. Or if you can, you deserve a Nobel Prize. They have to be measured.

Any theory of gravity needs $G$ in some form to relate how much spacetime curvature (or Newtonian "force" of gravity) is caused by how much mass/energy. E.g. we need to know if 1 kg of mass causes $1 \, g$, $1000 \,g$, $10^{-30} \, g$ of acceleration for a test mass. (It's closer to the last one, in our universe).

Also, regarding uncertainty of $G$ in gravitational wave detection, the LIGO/VIRGO measurements were direct measurements of strain, or ($\Delta$Length)/Length of space, and measurements of time. They do not rely on $G$. The part that relies on $G$ is estimating the masses and other features of the colliding black holes, and those parameters will have the correspondingly much higher uncertainty. Loosely speaking, the left side of the following equation was directly measured, and the right side was calculated from those measurements:

$$G_{\alpha \beta} = \frac{8\pi G}{c^4} T_{\alpha \beta}$$

Answer 2

Bronstein is often considered to have written the first dissertation on quantum gravity (1933). He introduced so-called cGh physics which I've seen more commonly described as the "Bronstein cube".

In this scheme, $(1/c)$, $G$, and $h$ are independent physical constants, which

• if they were in some sense "turned up to full",
  we would be in the realm of "Quantum Gravity" (quantum general-relativity).
• if we dial down (say) G to zero, we get to "Quantum Field Theory" (where gravitation is not important).
• and similarly for the other choices of parameters.

a figure from John Stachel's

• "A Brief History of Space-Time" (2003) https://www.researchgate.net/publication/252697584_A_Brief_History_of_Space-Time
• "Einstein's Intuition and the Post-Newtonian Approximation" (2006) https://www.bu.edu/cphs/files/2015/04/2006_Einstein_s_Intuition.pdf
• https://www.researchgate.net/figure/Bronstein-cube_fig1_241529454

Possibly useful: https://hsm.stackexchange.com/questions/14181/source-documents-for-bronsteins-cube-of-physics

Answer 3

So should Newton's empirical gravitational constant G be considered as the independent fundamental physical constant, say on the par with the Speed of Light?

I do not think so. In Einstein's theory G is a derived physical constant. Imagine a universe with matter that interacts only gravitationally (dark matter for example). Einstein's general relativity entails only two dimensional constants: the maximal possible force $\kappa^{-1}$, see [1], and the maximal possible velocity $c$ with which gravitational waves propagate. The Newton’s constant $G$ is then derived as $$G=\frac{\kappa~c^4}{8 \pi}. \tag{1}$$

[1] https://physics.stackexchange.com/a/713558/281096

Newton's famous equation $$F=G\frac{M_{1}~M_{2}}{r^2}, \tag{2}$$ can be written as $$F=\frac{G}{c^4}\frac{E_{1}~E_{2}}{r^2}=\frac{1}{8\pi} \kappa\frac{E_{1}~E_{2}}{r^2}. \tag{2}$$ Newton thought gravitation is caused by masses. Einstein showed that its source are rather their rest energies.

Answer 4

I'm going to take strong exception to your characterization of General Relativity as "highly theoretical" in contrast to Newton's "empirical" theory. In fact GR is more empirical, in the sense that it produces better predictions for things like Mercury's orbit; Newtonian gravity is a good approximation in many cases, but it is just an approximation.

Both GR and Newtonian gravity are built to be models of the real world, and so it should be no surprise that they both involve the same conversion factor $G$ (albeit in slightly different contexts). And since Newtonian gravity is a pretty good approximation in everyday cases, it's also no surprise that GR reduces to it in those cases -- Einstein explicitly made the theory so, because he wanted something that was realistic and produced good predictions for planetary orbits and other gravitational effects while also being compatible with special relativity.