This is a good question.
While there are analogies to electronic crystals, and much of the underlying concepts are the same there are significant differences. Sometimes it might help to look at how photonics crystals are computed numerically to illustrate some of the issues, or look at a special case such as one dimensional case. One big difference is that Photons are polarized and you can have a band structure that looks pretty different if the TM or TE modes are computed.
This arXive paper walks through the one dimensional case of a photonic crystal in detail. It also points out how the Berry phase changes with the band, and how the Wannier function are located (phase change) for different bands. It also points out that spatial the Wannier functions decay exponentially around the defect.
This paper specifically looks at using Wannier functions for defects in photonics crystals and how they can be computed more accurately when using numerical methods. It for example shows
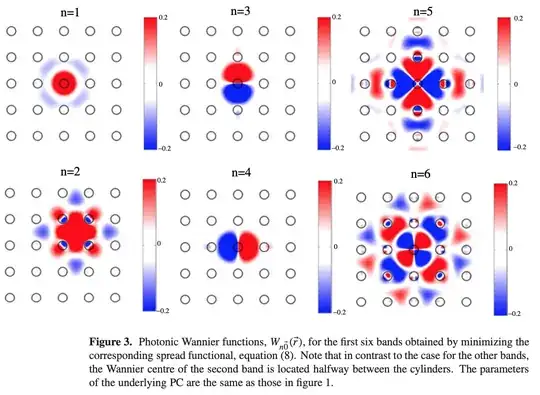
This shows the spatial localization of the photons in the materials. So for an electron in a crystal depending on the details of defect state we wouldn't usually think about it this way. We would think of it more as being a wave trapped in a potential well and would usually be in the lowest available energy state (unless maybe certain types of trapping where it might be metastable for a while). For the photons, I could populate the different modes by changing the frequency, or excite a lot of modes at the same time with a broad spectrum. You can also see the localization can have spatial extent especially for higher order modes.
So to directly answer your first question the Wannier functions are just a convenient basis set that can be used to 'solve' a photonic crystal. If there is a defect, you can use those functions to describe how the electromagnetic modes are spatially localized. How 'localized' depends on the band, or which mode or set of modes you are looking at. You can add as many photons to the mode as you want. If you have sufficient frequency resolution (narrow linewidth laser) you could try to selectively populate the modes. So in a sense you don't fill the bands like you do with electrons and Fermi-Dirac Statistics, but you can populate the modes.
Taking a look at the Wannier functions, you can see the phase at the center of zone changes. In the one dimensional case To compute the Chern Number from this paper it appear that you need to understand the Berry Phase and integrate over the Brillouin Zone.

So if I am interpreting this correctly, you don't need to know how 'filled' the band as you state in the electron case.

