If angle random walk (ARW) is the integration of white noise [°/s], why is its unit [°/sqrt(hr)] and not [°]?

Question

How can ARW have the unit [°/sqrt(hr)], if it's the integration of white noise which has the unit [°/s]? Shouldn't ARW be given in [°]?

I don't understand the correlation between these two. Besides, how can I imagine [°/sqrt(hr)]?

Answer 1

The angular random walk is a Wiener process in the angular dimensions, which means that the increments of the process are independent (uncorrelated) and that the differences follow a Normal Distribution (ND) with 0 mean and variance $t-s$ (with $t>s$), $$W_{t}-W_{s}\sim\mathcal{N}(0,t-s)$$ Since every ND can be expressed as a scaled & shifted standard ND (mean of 0, unit variance), then the above follows $$W_{t}-W_{s}\sim\sqrt{t-s}\mathcal{N}(0,1)$$ Taking this as an infinitesimal, we get $\mathrm{d}W\sim\sqrt{\mathrm{d}t}\mathcal{N}(0,1)$. Hence, there is a factor of sqrt(time) associated with the random variable, rather than simply time or unitless.

Books on stochastic processes will almost surely provide a better answer than the fast-and-loose one here, so it would be worth your time investigating that branch of mathematics (for some pointers on a book, see this physics Q&A)

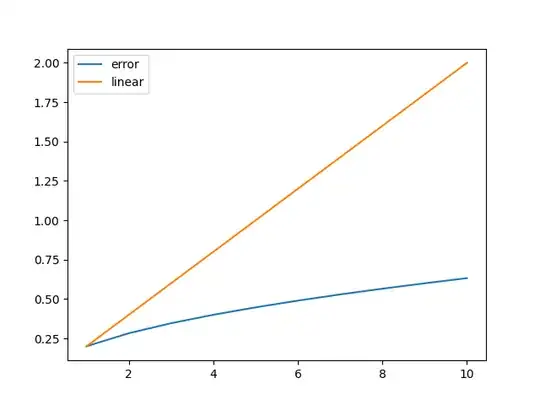
I think a good way to think of this square-root-time relationship is that the accumulated deviation is not constant and not linear, but somewhere between. For instance, consider an ARW of $0.2^\circ/\sqrt{\text{hr}}$, then after 1 hour the standard deviation is $0.2^\circ$. After 2 hours, it's $\sqrt{2}\cdot0.2^\circ=0.28^\circ$. Keep on going and after 10 hours, the accumulated deviation is now $0.63^\circ$. Had this been a linear process, we'd have a deviation of $2^\circ$, as depicted in the figure I made with Python below,