2

Let's say I have a uniformly charged wire with some constant linear charge density. Along a line parallel to the $z$-axis and passing through $(0,y,0)$ and asked to find an electric field at a point $(p,q,r)$. Then the vector should be $p \textbf{i} +(q-y)\textbf{j}+r\textbf{k}$. My books say the field has no $z$ component and it takes vector as $p\textbf{i}+(q-y)\textbf{j}$. Can someone explain this?

failedtitration
  • 71
  • 8
Sai
  • 71

1 Answers1

4

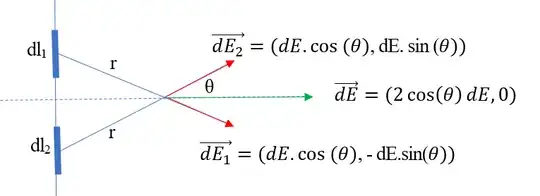
It is a question of symmetry. If the source (charge distribution) is z independent (the same for any z), then the field does not depend on z. It can be mathematically proven, but a simple drawing is sufficient. Sum of two electric fields

Consider two elementary segment of length $ dl_{1}$and$ dl_{2}$. They carry the charge $ dq= \lambda dl_{1}= \lambda dl_{2} $ This charges create at the M two electric fields:$ \overrightarrow{d E_{1} } $ and $ \overrightarrow{d E_{2} } $. The electric field intensity only depends on the charge and distance between source and point of observation. So $d E_{1}=d E_{2}=dE= \frac{dq}{4 \pi \varepsilon _{0} r^{2} }$ At the point of observation, the electric fields add up. The vertical components cancel out and one gets: $ \overrightarrow{dE} =2.cos( \theta )dE \overrightarrow{i} $

Shaktyai
  • 2,020