Does the event horizon always stay below you in the frame falling freely with you in a black hole?

Question

Imagine you fall freely into a black hole. You place small test masses inside your frame with a fixed distance between them.

What will we see? The only force inside your frame is the tidal force. The closer to the center of the hole you get (or better, the center accelerates towards you, actually staying hidden behind the alleged horizon which gets closer and closer, so I guess, hitting you when you hit the hole(?)), the bigger the force. Falling through the horizon you notice nothing special if the mass of the hole is big enough.

The further you look towards the center the faster the test-masses accelerate away from you. Light from the test'masses can reach you (I guess, but I'm not sure).

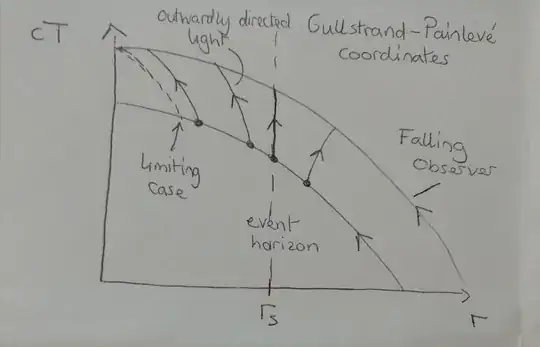
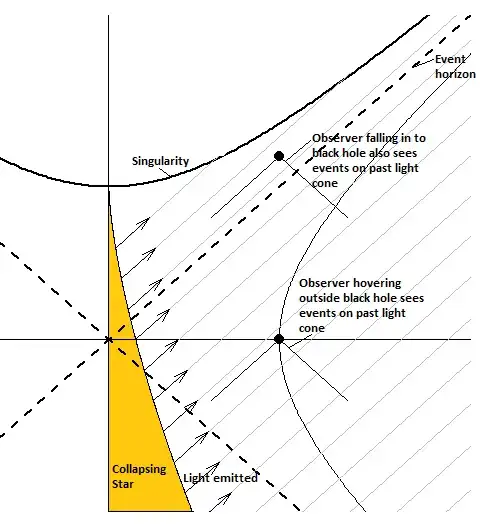
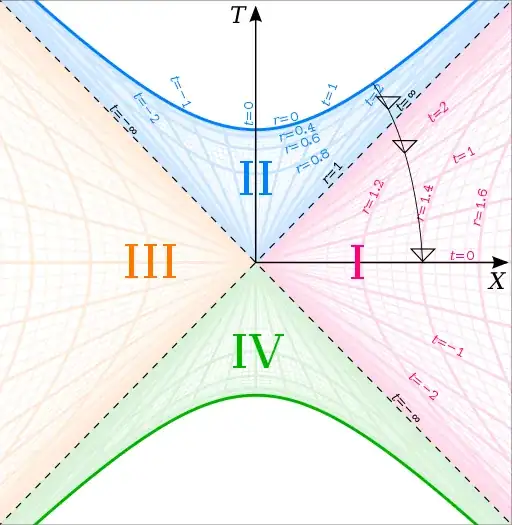
So it seems there is a radial distance from behind which light can't reach you. In other words, there is an event horizon in front of you. Of course you won't be able to get out of the hole to reach the universe you fall from into the hole. That contact is lost forever and in the small amount of time that has passed on your clock the universe has run fast forward. So for the outside world you seem to freeze on the horizon situated on the outside radial r-coordinate. But in your falling frame there seems to be an horizon that's situated always below you. And by "always" I mean the small amount of the proper time that's left for you.

What can we say about this horizon? Is it really there?

Answer 1

There is no moving event horizon for a falling observer. It is still the case that this observer cannot receive information about events inside THE event horizon until they have also passed inside it.

Once inside the event horizon they can receive information from events inside the event horizon, but only from events that happened at a larger radial coordinate, because light can only travel towards a smaller radial coordinate inside the event horizon.

There is of course a limit provided by their inevitable coincidence with the singularity. This may prevent the receipt of signals that arise from other observers or objects that fell into the black hole earlier from reaching them, depending on how much earlier they fell. As the original falling observer proceeds towards the singularity, this limiting time gap becomes shorter and shorter.

But this is not an "event horizon". There is no fixed radial coordinate from below which no signals can be received (other than their own radial coordinate).

I think problems like this are most easily studied in Gullstrand-Painleve coordinates, where the time coordinate corresponds to the proper time experienced by an observer falling from infinity.

I provide a rough sketch of the problem below, showing the world-lines of two observers falling into a Schwarzschild black hole along the same radial trajectory. The first falling observer signals to the second and the outwardly-directed light ray geodesics are shown.

The outwards directed light is vertical when emitted or received at the event horizon. Inside the event horizon, outwardly -directed light moved towards smaller $r$. The second observer will only receive light from the first if it was emitted from greater than their $r$ coordinate when the light is received. A limiting case is shown where the light just reaches them at the singularity.

Answer 2

The usual presentation of black holes being black because light can't escape is misleading. When you look towards a black hole, what you see is determined by your past light cone, which the black hole's gravity twists round to point into the distant past. What you are looking at is the entire history of the black hole since its formation, and everything that has fallen in to it. It only looks black because it is so spread out and red-shifted out of the visual range.

The event horizon is not some impenetrable, opaque black surface. Outside the hole you can't see it at all because it is always in the future, and you can't see or look at the future. What you see instead when you look in that direction is the stretched-out light from the collapsing star, that has hovered on the boundary for a few million years before finally crawling up out of the gravity well and out to your eyes. Even after you fall in, you still see the same light from matter that fell in millions of years before you, that the collapsing star emitted after it fell in.

What you see (and the gravity you feel) is always determined by events on the past light cone of the observer. This stretches back to the collapsing star that formed the black hole, and everything that fell in subsequently. The blackness of a black hole has nothing to do with the event horizon preventing light escaping, and everything to do with the fact that the last few microseconds of light emitted are being stretched out over billions of years.

Answer 3

So it seems there is a radial distance from behind which light can't reach you.

This is incorrect. It is easiest to see in Kruskal–Szekeres coordinates:

What makes these coordinates so useful is that in these coordinates light always travels along 45 degree diagonal lines.

Notice the vertical line labeled $T$ which is the line $X=0$, which is the center. For any event inside the event horizon, i.e. in region II, there is a 45 degree line to some event on the $X=0$ line. So at each event an observer can receive light from the center.

Notice that the $X=0$ line corresponds to the Schwarzschild coordinate $t=0$ line, not the Schwarzschild $r=0$ line. That is because inside the horizon the Schwarzschild $r$ is timelike and the Schwarzschild $t$ is spacelike. So “towards the center” is in the direction of decreasing $t$. The singularity is not at the center, it is in the future, at the time $r=0$