What is canonical momentum?

Question

What does the canonical momentum $\textbf{p}=m\textbf{v}+e\textbf{A}$ mean? Is it just momentum accounting for electromagnetic effects?

Answer 1

The canonical momentum $p$ is just a conjugate variable of position in classical mechanics, in which we have the relation $p=\frac{\partial L}{\partial \dot{r}}$. When making the transition to quantum mechanics, we substitute $p$ with an operator $-i\hbar\nabla$ in the Hamiltonian; similarly, we substitute $r$ by $i\hbar \nabla_p$ in momentum representation.

The kinetic momentum is named "kinetic" because it represents the velocity of the particle in classical mechanics. When we are talking about the quantum mechanical expectation values, kinetic momentum $\vec{P}$ should satisfy

$$\frac{d\langle\vec r\rangle}{d t}=\frac{\langle\vec{P}\rangle}{m}.$$

Another significant point about them is that the kinetic momentum is a gauge invariant quantity, while the canonical momentum depends explicitly on the gauge choice.

Neither the canonical $\hat p=-i\hbar\nabla$ nor the kinetic momentum $\hat{P}=-i\hbar\nabla-q\vec{A}$ is a conserved quantity in the general case.

Consider the Hamiltonian in an electromagnetic field:$$H=\frac{1}{2m}(\hat p- q \vec{A})^2+q \varphi.$$ One can check that $$\frac{d\langle \vec P \rangle}{dt}=q\langle \vec E\rangle+\frac{q}{2m}\langle(\hat p\times \vec B-\vec B\times \hat p)\rangle-\frac{q^2}{m}\langle\vec{A}\times\vec{B}\rangle$$ and $$\frac{d\langle \vec p \rangle}{dt}=-q\langle\nabla\varphi\rangle+ \frac{q}{2m}\sum_j\langle(\nabla A_j) p_j+p_j(\nabla A_j)-2qA_j\nabla A_j\rangle,$$ where $$\vec E=\nabla \varphi-\partial\vec A/\partial t$$ $$\vec B=\nabla\times\vec A.$$

Thus, you can see in general they are not conserved. Even in the very special case as @Frederic Brünner points out: $\vec A$ is position independent.

So forget about the conservation of both, they may be conserved only in some very special cases.

Answer 2

Imagine this situation:

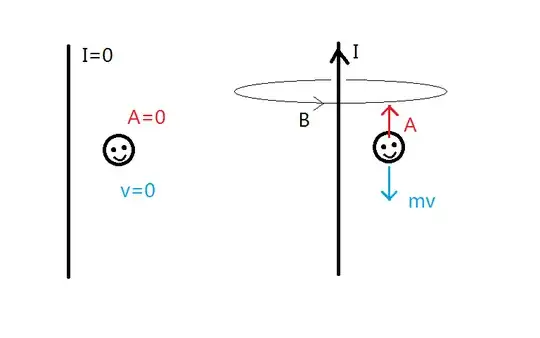
at time t=0, we have a infinite long straight wire with current zero, and a charged particle q with zero velocity.

at time t=T, we make the current to be I, thus we have a $ \mathbf{B}$ field, and $ \mathbf{A}$ field.

during this process, $ \mathbf{A}$ is build up from zero to some value, therefore we have induced electric field $ \mathbf{E}= - \frac{ \partial \mathbf{A}}{\partial t}$

$\Delta (m\mathbf{v})=\int \mathbf{F} dt = \int q \mathbf{E} dt =\int q \frac{ - \partial \mathbf{A}}{\partial t} dt $

assume this process happened very fast, the particle almost stays at the same position, $ \frac{ \partial \mathbf{A}}{\partial t} =\frac{ d \mathbf{A}}{d t}$

then

$\Delta (m\mathbf{v}) =\int q \frac{ - d \mathbf{A}}{d t} dt = - q \int d \mathbf{A} =-q \Delta \mathbf{A} $

$ \Delta ( m \mathbf{ v } +q \mathbf{A}) =0 $

$ m \mathbf{ v } +q \mathbf{A} = constant $

Answer 3

The whole problem starts when you try to do electromagnetism with the Lagrangian because you can't write the magnetic field in terms of a potential. However we CAN write it in terms of a vectorpotential $\vec{A}$:

$\vec{B} = \nabla\times\vec{A}$.

It seems that this is usefull and can be used to derive the appropriate Lagrangian and Hamiltonian which are given and checked here.

It seems (from the calculations given in the link) that to include the magnetic field, we need to replace our momentum with:

$\vec{p}-q\vec{A}$.

By replacing the momentum by this term, you are able to do Lagrangain and Hamiltonian mechanics (which work with potentials) for magnetic fields (which can't be written in terms of a potential).

For electric fields you can still include them by using the electronic potential.

Answer 4

Yes, it accounts for the effect of the vector potential on a moving charge. But there is also a more fundamental role that it plays: assuming position-independent vector potential, the canonical momentum is a conserved quantity, while the "normal" (or kinetic) momentum (mass times velocity) is not.

Answer 5

In Lagrangian mechanics, "momentum" is just a conserved quantity, and is the derivative of the Lagrangian with respect to velocity ($\frac{dL}{d\dot{q}}$). For the case of a point charge traveling through a uniform magnetic field $\mathbf{B}$, $\mathbf{p} = m \mathbf{v}$ simply isn't conserved anymore, as the charge travels in a circular path due to the magnetic field, causing its momentum to constantly change direction. A quantity known as the canonical momentum, $\mathbf{P} = m\mathbf{v} + e \mathbf{A}$ ends up being conserved throughout the charged particle's trajectory. (Setting the total time derivative of the canonical momentum equal to zero simply results in $m \mathbf{a} = e \mathbf{v} \times \mathbf{B}$, which is just the expression for magnetic force.) In short, the canonical momentum is simply "the quantity that is conserved" in electromagnetic interactions, while the kinetic momentum is just the product of mass and velocity.

Answer 6

The canonical (total) momentum is the sum of the kinetic (mechanical) momentum and the potential momentum. Potential momentum occurs only if the potential energy depends explicitly on velocity.