Yet another perpetual motion machine: does this imply large selective membranes are not possible?

Question

So I was just thinking about the buoyant force and came up with what seemed like a simple perpetual motion based on it. Obviously such things are not physically possible so I'm trying to figure out where this machine goes wrong.

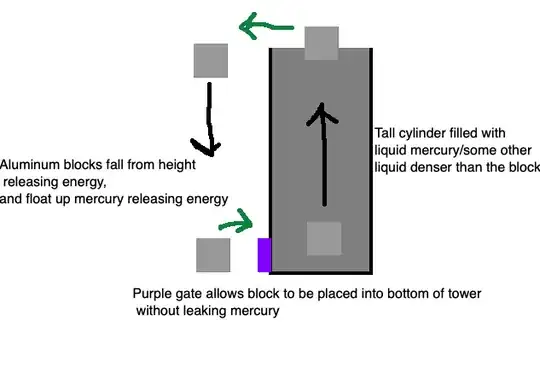
So, the schematic is to have a large tower consisting of some high density liquid (we use mercury in the example) and to have a block (i choose aluminum) which is denser than the ambient surrounding liquid (air) and less dense than the tower's liquid.

So, the principle of operation would be to get the block into the bottom of the tower via a gate which I can pretend is a selective membrane that only allows aluminum blocks in but no mercury out (some energy is spent pushing it through this membrane)

Once the block is inside it floats up doing work equal to $(m_\text{displaced_fluid} - m_\text{block})gh$ and at the top we then spend some energy to knock it off the top of the tower where the block now is in free fall and capable of doing work equal to $(m_\text{block})gh$

So analysis:

1. Knocking the block off the top of the tower can be made to take a very small amount of energy (and or make the tower very tall) so it can't be the primary point of waste here.

Which leads us to conclude

2. The "purple gate" our apparatus for pushing the block is not physical?

This requires some energy to push the block in i.e. $\text{volume}_{block} \times \text{fluid density}$ but if the tower is made sufficiently tall then that energy expense would be far less than what is generated when the block floats up. I find this hard to believe since selective membranes certainly can operate at the microscopic level (our cells use them all the time).

Third idea?

Is it somehow possible that the selective membrane is okay but the energy required to get the block through the membrane is proportional to the height of the tower? I could imagine its possible to estimate this if we assume the block displaces the fluid directly above it, which displaces the fluid above that etc etc etc meaning the amount of fluid displaced/moved is now proportional to the height of the tower. But I am no longer confident that analysis is correct.

Answer 1

Many devices that seemingly constitute perpetual motion machines contain two parallel paths that clearly provide excess energy each way.

• One example is a capillary wick that lifts water to be dispensed from a height.
• Another is an arrangement of permanent magnets that raise a magnetic object to then release it from a height.
• Yet another is a tall container of high-density fluid in which objects tend to float to again be dropped from a height through a low-density fluid (patent application example; buoyancy motor #4 from the Museum of Unworkable Devices; previous question with nice figures; related question about the feasibility of buoyancy to usefully lift heavy objects).

It's easily demonstrated that the one-way mechanisms do indeed provide the desired motion. And it's certainly conceivable that the spontaneous motion in the second step—maybe even the first step too—could run an engine, providing work. It's also reasonable that the paths can be made arbitrarily long to scale up the recovered energy as needed. Finally, it's undisputed that the transfer mechanisms at the top and bottom are straightforward and require only a small energy expenditure.

Oh wait. That last point is disputed.

In the first two examples, and related examples, we run into the problem that a system that strongly attracts and propels one's working material doesn't easily let go of that working material. (Water attracted to a hydrophilic surface doesn't easily drip from that surface; magnetic objects pulled up by magnets aren't easily separated from those magnets.)

But what about the buoyancy design? The floating objects can be pushed over to the low-density-fluid shaft (let's just assume it contains air) with ease. And can't we design an airlock at the bottom so they can be slid into the high-density-fluid shaft (let's just assume it contains water) with ease?

No. Regardless of what mechanism one uses to reinsert the object at the bottom cyclically, one must move an equal volume of water out of the way. One can't just let it drain out of the airlock, because that precludes indefinite cyclic operation; the water would soon be depleted.* One must pump it from the bottom to the top, which is much harder if the tower was designed to be very tall (ostensibly to render energy overheads negligible).

*If refilling occurs via rain or a waterfall, for instance, that's just extracting energy through hydropower; the buoyancy mechanism is unnecessary.

In fact, because of real-world inefficiencies, the insertion work required always exceeds that total work obtained from the rising and falling steps. The very best one can do is a net energy production of zero. These (unworkable) devices are perpetual motion machine of the first type.