0

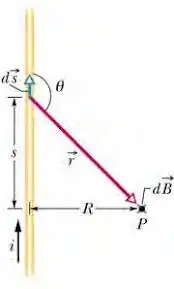
The following image is from Halliday and Resnick, Fundamentals of Physics. The magnetic field at P due to the current element is shown as being directed into the page. The textbook and other sources state that the direction of the cross product in the Biot-Savart law gives the direction of the magnetic field at that point, but I can't see how this can be deduced from the formula alone. For the electric field created at a radial distance by a point charge, there is a radial unit vector which tells us the direction of the field along that line. I don't see which part of the Biot-Savart law contains information about the direction of the magnetic field at a radial distance away from the current element. Is this a generally accepted property of cross products, or is there no way to express this information in a formula?

enter image description here

Thomas Fritsch
  • 42,352
Piksiki
  • 75

2 Answers2

1

According to the Biot-Savart law the current element $I\ d\vec{s}$ gives this contribution to the magnetic field $\vec{B}$ at point $P$: $$d\vec{B}=\frac{\mu_0}{4\pi}\frac{I\ d\vec{s}\times\vec{r}}{r^3}$$

From this formula you see that $d\vec{B}$ has the direction of $d\vec{s}\times\vec{r}$. Given the direction of $d\vec{s}$ (the green arrow) and $\vec{r}$ (the red arrow) and using the right-hand-rule for the direction of the cross product you find $d\vec{s}\times\vec{r}$ and thus $d\vec{B}$ is pointing into the page.

Thomas Fritsch
  • 42,352
0

I'm not sure I understand the question... It's just a basic property of the cross-product: $\vec{a}\times\vec{b}$ is perpendicular both to $\vec{a}$ and $\vec{b}$ (except of course if $\vec{a}$ and $\vec{b}$ are colinear, in which case the product is simply zero).

If your question is more about why the magnetic field has this property, it's a bit more subtle. $\vec{B}$ is a pseudovector.

Miyase
  • 6,342