Introduction:
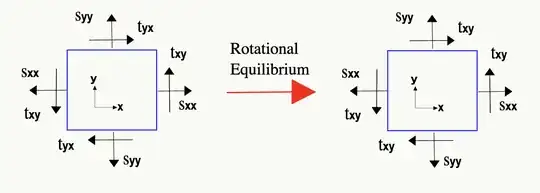
According to the theory, the stress tensor should be symmetric. On This page, and on many others, the explanation is: Taking the rotational equilibrium around the center of this 2D square yields, that tao_xy should be equal to tao_yx:
I am confused by this:
Why do we assume tao_xy on the right of the square to be equal to tao_xy on the left of the square? Couldn't it be different? Wouldn't this assumption make tao_xy and tao_yx equal and constant in throughout every point of the body?
Furthermore:
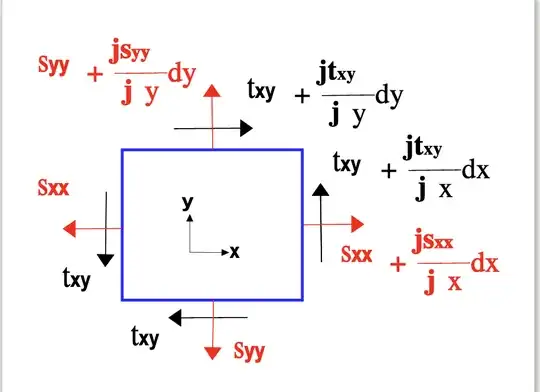
In a different post, they showed this figure:
This picture is more understandable for me. As we can see, the right tao_xy differs from the left tao_yx. But given this circumstance, the proof for the symmetry of the stress tensor doesn't work anymore. What am I missing?