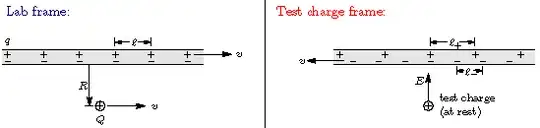
Imagine we have a test charge and we push it, reaching a constant velocity of $u$. Now the electrons inside of the cables reach a velocity of $v$. Our goal is to measure the electric field that the test particle would measure from their own frame of reference.
Assuming that the cable has a linear charge density $\lambda$, that is the sum of the density of positive and negative charges. $$ \lambda = \lambda_{+} -\lambda_{-} $$ Also, the velocity at which the electrons are moving in the particle's frame of reference is given by: $$ v_- = \frac{v - u}{1 -\frac{uv}{c^2}} $$ Where $v$, is the velocity of the current at the lab frame. For the positive charges the equation is more or less the same: $$ v_+ = \frac{v + u}{1 +\frac{uv}{c^2}} $$ $$ \lambda_0 = \frac{q}{\ell_0} \rightarrow \lambda(v) = \frac{\lambda_0}{\sqrt{1 - \frac{v^2}{c^2}}}\\ \lambda_+ = \frac{\lambda_0}{\sqrt{1 - \frac{(v_+)^2}{c^2}}}\\ \lambda_- = \frac{\lambda_0}{\sqrt{1 - \frac{(v_-)^2}{c^2}}} $$ Rearranging we obtain the following: $$ \lambda_+ = \frac{\lambda_0 (c^2 + uv)}{\sqrt{(c^2-u^2)(c^2 - v^2)}}\\ \lambda_- = \frac{\lambda_0 (c^2 - uv)}{\sqrt{(c^2-u^2)(c^2 - v^2)}}\\ \lambda = \frac{\lambda_0 (c^2 + uv)}{\sqrt{(c^2-u^2)(c^2 - v^2)}} - \frac{\lambda_0 (c^2 - uv)}{\sqrt{(c^2-u^2)(c^2 - v^2)}} = \frac{2 \lambda_0 uv}{c^2\sqrt{1-\frac{u^2}{c^2}} \sqrt{1-\frac{v^2}{c^2}}} $$ Let's define the following to simplify the expression: $$ \bar{u} \equiv \frac{u}{\sqrt{1 - \frac{u^2}{c^2}}}\\ \bar{v} \equiv \frac{v}{\sqrt{1 - \frac{v^2}{c^2}}} $$ $$ \lambda = \frac{2 \lambda_0 \bar{u}\bar{v}}{c^2} $$
Then, we will have to know what is the Electric Field generated by a cable. $$ \iint{\mathbf E \cdot d \mathbf A} = \frac{q}{\varepsilon_0} \\ | \mathbf E| = \frac{\lambda}{2 \pi \varepsilon_0 R} \\ | \mathbf E| = \frac{2 \lambda_0 \bar{u}\bar{v}}{2 \pi c^2 \varepsilon_0 R} $$ Knowing that $\mu_0 = \frac{1}{\varepsilon_0 c^2}$ and $I = 2 \lambda v$, where $I$ is the current intensity. $$ | \mathbf E| = \bar{u} \frac{\mu_0 \bar{I}}{2 \pi R} $$ For finding the force exerted on the particle, we have to use the definition of electric field: $$ |\mathbf F| = q |\mathbf E| \\ |\mathbf F| = q\bar{u} \frac{\mu_0 \bar{I}}{2 \pi R}\\ |\mathbf B| = \frac{\mu_0 \bar{I}}{2 \pi R} $$ Having the following: $$ |\mathbf F| = q \bar{u} |\mathbf B| $$
Two questions come to my mind with this derivation. It has been concluded that magnetism is a consequence of Special Relativity. But, how would you derive the same equations assuming that the positive charges are at rest; I could only arrive to this result by assuming that, both the protons and electron are moving at the same speed but with opposite directions (because it makes the math easier). And secondly, in this equation:
$$\lambda = \frac{2 \lambda_0 uv}{c^2\sqrt{1-\frac{u^2}{c^2}} \sqrt{1-\frac{v^2}{c^2}}} \ ,$$
we get two Lorentz factors one for $u$ and the other one for $v$, making the final equation to be like "the corrected" form of the magnetic force for Special Relativity, that (here is my question) I assume appears as a consequence of the theory; like a restriction, reminding us that we cannot go faster than the speed of light, no? If not, what is the meaning of these two Lorentz Factors?