What is the motion of a pendulum for large angles?

Question

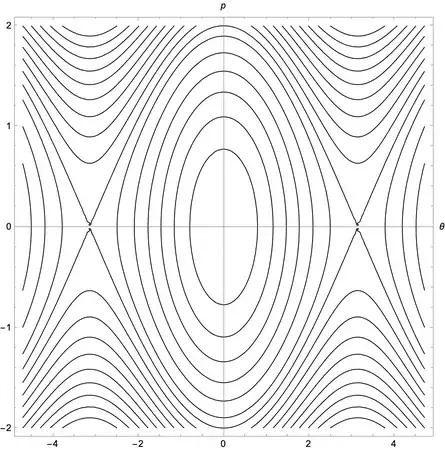
We are given the second-order (non-linear) differential equation describing the pendulum $$\ddot x + \frac{g}{l}\sin(x) = 0.$$ One usually approximates this physical system with the one in which the angle $x\rightarrow 0 $ leading to a second order linear differential equation $\ddot x + \frac{g}{l}x= 0$ which leads to the simple solution of the harmonic oscillator. In case we do not do this approximation, i.e. we allow the pendulum to swing for large angles, what would be the solutions for the equations of motion? Will the pendulum still oscillate on a vertical plane? Will it whirl around the axis set by the thread? Will the system consisting of thread and mass whirl together around the vertical axis? In a book it says it will whirl over the top which I do not understand exactly which motion is meant.

Can you elaborate on one or the other of my questions?

Answer 1

In case we do not do this approximation, i.e. we allow the pendulum to swing for large angles, what would be the solutions for the equations of motion ?

If the amplitudes are large then we get: $$\theta(t)=\mathrm{am}\left( \frac{v_0 t}{2l} , \frac{4gl}{v_0^2} \right)$$ where $\mathrm{am}$ is the Jacobi amplitude function and $v_0$ is the velocity at $\theta=0$.

Answer 2

Multiplying the equation with $\dot{x}$, we get: $$\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{1}{2}\dot{x}^2-\frac{g}{l}\cos(x)\right) =\left(\ddot{x}+\frac{g}{l}\sin(x)\right)\dot{x}=0.$$ Therefore there exists a constant $E$ (the energy of the pendulum) with: $$\frac{1}{2}\dot{x}^2-\frac{g}{l}\cos(x)=E.$$ This results in an elliptic integral that is pretty hard to compute. But using the theory of Riemann Surfaces, an exact solution to this differential equation can be obtained as: $$x(t)=\arccos(\wp_\Lambda(t-t_0))$$ with the Weierstraß $\wp$-function and a suitable lattice $\Lambda\subset\mathbb{C}$. The derivation in detail is given in Riemann Surfaces by Simon Donaldson (See here) on page 77 to 83.

Answer 3

The motion is still periodic: it's just not harmonic motion. Possibly the easiest way to see this is by plotting contour curves of constant energy $$ E=\frac{p^2}{2m}-\cos(\theta) $$ Because the motion is restricted to a curve in the $(\theta,p)$ plane, closed curve indicate period motion since, after some time $t$, a curve passing through $(\theta_0,p_0)$ will eventually pass again through $(\theta_0,p_0)$, defining a period of the motion.

What the plot doesn't tell you is how the amplitude is related to the period. For this you use a well known expression which yields an integral that cannot be expressed in terms of elementary functions and must be evaluated numerically, although it is possible to plot $T$ as a function of the maximum amplitude $\theta_{max}$. Plotting $\frac{T}{4}\sqrt{\frac{g}{\ell}}$ as a function of the maximal angle $\theta_{\max}$ yields the curve

so that, for small angles, the period is very nearly that $1$, meaning that $T\approx 2\pi\sqrt{\ell/g}$. The curve rises steadily but slowly until about $\theta_{max}=\pi/2$, at which point the increase with of $T$ with $\theta_{max}$ is much more pronounced. Note that, at $\theta_{max}$ approaches $\pi$, $T\to \infty$.

Answer 4

If the starting angle is smaller than pi or 180° it will still oscillate but not a harmonic oscillation. If the starting velocity is large enough it will rotate around the axes on top, but slow on top and fast at the bottom. You have no solution with the known functions, so the integration is done numerically. All the motions are in the same plane.