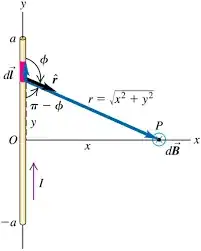
In this figure, how will the wire elements between O&a and O&-a affect the magnetic field at point 'P' which lies at a distance x from point O? Because none of the field lines created due to the wire elements between points a and O and points -a and O seem to pass through point P. Maybe I'm lacking some important concept.
 Consider a point 'P' at some horizontal distance 'x' from the middle point of the wire. If we draw the magnetic field lines due to an infinitesimally small current-carrying wire element, then they don't seem to pass through point 'P' but still, we say that it affects the magnitude of the magnetic field vector at point 'P'...why?...because in order to do so the field lines due to all the tiny elements on the wire should pass through point 'P'...
Consider a point 'P' at some horizontal distance 'x' from the middle point of the wire. If we draw the magnetic field lines due to an infinitesimally small current-carrying wire element, then they don't seem to pass through point 'P' but still, we say that it affects the magnitude of the magnetic field vector at point 'P'...why?...because in order to do so the field lines due to all the tiny elements on the wire should pass through point 'P'...
- 53
- 6
2 Answers
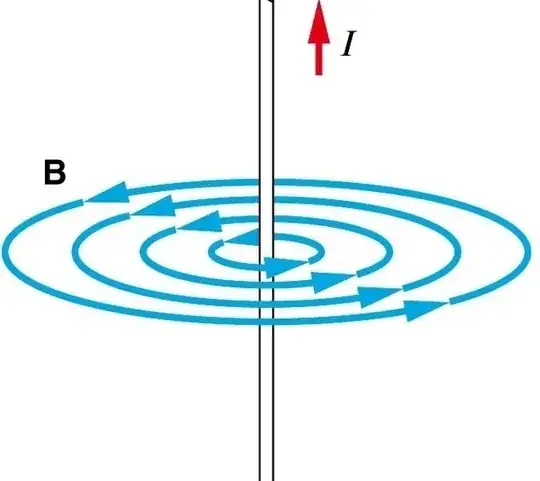
The field lines are concentric circles in all plains perpendicular to the current density shaded in purple.
I have drawn smaller circles to indicate magnitude, but they extend to infinity.
Hence the field from the current density reaches point p
- 7,016
Physically speaking the current could not just end like you show. There should be charging on the apex of the wiring, otherwise wire should go somewhere. Anyway the Biot-Savare law stands that in vacuum
\begin{equation} \vec{B} = \frac{\mu_0} {4\pi}\int_{wire} \frac{I \vec{dl}\times \vec{r'} }{ |\vec{r'}|^2 } \end{equation} where $\vec{r'}$ is the vector from the local current to the observation point. So if you have a finite current source you could formally integrate over your finite wire in order to get the magnetic field.
- 750
- 4
- 19