How does earthing a conductor make its potential zero?

Question

My teacher explained about the earthing of a conductor. She said that when we connect a conductor with the Earth, its potential goes to zero because the Earth always has zero potential; however, she never explained why this happens, so I have tried to understand this by reasoning with electric fields.

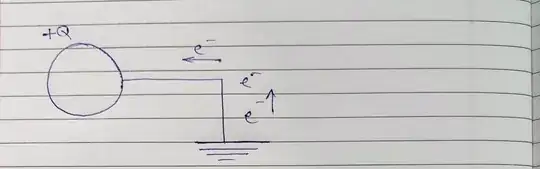
Suppose I have a conductor with $+Q$ charge on its surface. When I connect the conductor with Earth, the conductor's potential ($V$) becomes zero.

Now, the positive charge will create an electric field that will attract the electrons from Earth, which move to the conductor. As the conductor gains the electrons, the positive charge will keep decreasing. At the same time, Earth will have a positive charge (as it is losing its electrons). However, the electric field due to Earth is almost zero since its radius is much larger. Usually, the electron should keep moving until the net electric field becomes zero between the conductor and Earth; here, the Earth has zero electric field, so electrons will keep moving to the conductor until the net charge becomes zero.

Is my intuition correct here? Is it valid for every conductor of any shape and size?

Answer 1

Yes, you are correct.

The Earth behaves like a very large capacitor¹. For a capacitor the potential is:

$$ V = \frac{Q}{C} $$

so for any finite charge $Q$ as the capacitance $C \to \infty$ the potential $V \to 0$. And as you say the Earth acts as a very large capacitor because it's big. The capacitance of a sphere is given by:

$$ C = 4 \pi \epsilon_0 R $$

where $R$ is the radius, and for the Earth $R$ is about $6.4$ million metres.

---

¹ We should be a little careful about defining what we mean by capacitance. In this context I mean the self capacitance i.e. if you take an isolated object like the sphere in your diagram and put a charge $Q$ on it then $V = Q/C$ gives us the potential relative to infinity.

Note that this is different from a parallel plate capacitor where $C$ is the mutual capacitance i.e. it gives the potential of the plates relative to each other not relative to infinity. As a general rule the self capacitance is much smaller than typical mutual capacitance values.

Answer 2

Your reasoning is correct and indeed independent of the shape of the conductor.

Answer 3

When you attach a conductor to Earth the conductor comes to whatever potential the Earth is.

If we conventionally say the Earth is 0 V then attaching a conductor to Earth will bring the conductor to 0 V. But there is no rule saying we have to take this convention.

Sometimes people take the convention that 0 V is at infinity. In that case it is not obvious what voltage Earth is as it would depend on the total charge on the Earth and in the atmosphere and I don't know whether that amount is positive or negative (or if it fluctuates about 0).

Answer 4

Adding some numbers to illustrate that the Earth (almost completely ) "discharge" the sphere.

The potential of the Earth can be used as the reference potential and this is often defined as $0\,\rm V$.
As such it would be desirable that the potential of the Earth relative to say, the potential at infinity, does not fluctuate very much.

The capacitance of an isolated sphere is $C = 4 \pi \epsilon_0 R$ where $R$ is the radius of the sphere.
The "other" plate of the capacitor is taken to be infinity.

Putting in numerical values the capacitance of the Earth is approximately $710\,\rm \mu F$ and that of a sphere of radius one centimetre is approximately $1\,\rm pF$.
Suppose an isolated one centimetre sphere is charged to a potential of $1000 \,\rm V$ relative to infinity, then the charge on the sphere will be $1\,\rm nC$.

Although not true in practice, suppose the isolated Earth is uncharged and so its potential, relative to the potential at infinity, is $0\,\rm V$.

If the charged one centimetre sphere is connected to the Earth with a conductor, because of the difference in potential between them a current will flow until the potentials of the Earth and the one centimetre sphere are the same.
Almost all of the charge of $1\,\rm nC$ will now reside on the Earth which will then have a potential of approximately $1.4 \times 10^{-6}\,\rm V$ relative to the potential at infinity.

In general after connecting the Earth and the sphere together

$V_{\rm final} = \dfrac {Q_{\rm final, Earth}}{C_{\rm Earth}} = \dfrac {Q_{\rm final, sphere}}{C_{\rm sphere}} =\Rightarrow \dfrac {Q_{\rm final, Earth}}{R_{\rm Earth}} = \dfrac {Q_{\rm final, sphere}}{R_{\rm sphere}} $

where $Q_{\rm final, Earth}+Q_{\rm final, sphere}= Q_{\rm initial, sphere}$

Answer 5

Earth potential is the reference value. You can assume that it is 0V localy. But in larger scale the earth potential can differ. Why? Because there always is resistance - earth resistance. When you inject current into earth (powerlines, industry, lightning strikes) you cannot forget about the Ohm Law. Injection point and its surrouding can be described with potential / voltage gradient.