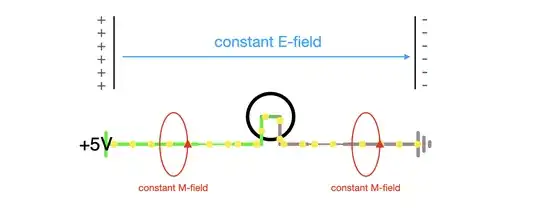
I don't understand how energy is being transferred in a DC circuit. For example here I have a simple circuit powered by a constant voltage. Some form of energy is being transferred from the source to the light bulb and the light bulb lights up.
A constant voltage means there is a constant electric field between the terminals of the light bulb. A constant current means there exists a magnetic field of constant magnitude looping around the wire. If both the electric field and magnetic field is constant, there cannot be EM waves propagating along the wire to deliver energy to the light bulb.
If the energy is delivered by the constant electron drift, something has to move a lot faster than the drift current itself to signal or deliver the energy to the load (otherwise the light bulb wouldn't light up instantaneously). But again, both the E-field and M-field are constant, there cannot be waves propagating.
So what is delivering energy in a DC circuit and how does it work?