-1

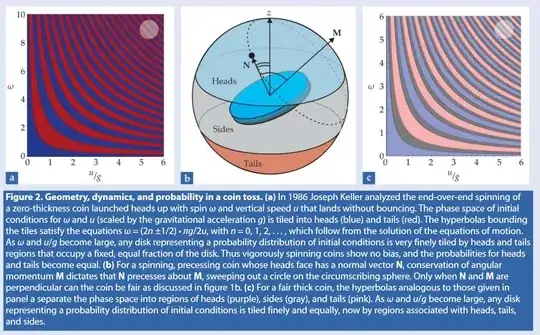
Let's just take a typical coin flip where a person flips the coin off their finger into the air (some reasonable distance, say 30-40 cm or so), catches it, and opens their hand to reveal one side face up.

I understand that it only takes one bit of information to store the outcome, but how much information would be required to store all the information necessary to predict the outcome perfectly? I mean absolutely perfectly with zero error. Of course, this is (probably) physically impossible.

I am thinking that we'd need quite specific information about the positions and velocities of a large number of particles, something like every molecule within a 1 meter radius of the spatial region. My guess is that it is too much information to store in any physically feasible computer -- and much less physically possible to even gather all the necessary data in the first place before the coin gets flipped.

The human body will account for the vast majority of the matter, and that is something like $10^{27}$ atoms, so I can only imagine that is the number of bits we'd need to store, give or take a few orders of magnitude. A conservative estimate is probably like at least $10^{18}$ bits or somewhere on the order of a few hundred petabytes. But that would probably only give a very high degree of accuracy with perfect accuracy requiring the entire state of the universe or at least a much larger spacetime region.

Update/edit: Since the question was closed, I'll try to elucidate the question and answer here. The question is: "how much information is required to predict a coin flip perfectly, where a person flips it and catches it?" And the answer seems to be knowing the complete state (and history) of the universe, which is at lest a finite but very large amount of information but possibly infinite. It is likely the case that this is even in-principle and hypothetically fully physically impossible. Though it is physically possible to predict a coin flip with a very high degree of accuracy under controlled conditions (e.g. see the Diaconis paper). The specific setup here where a human flips it and catches it is probably very hard to control/monitor and thus may require an unfeasible experimental setup. If it is just a person flipping it and having it land on a stable surface, then that could probably be feasibly predicted to a high degree of accuracy, e.g. 99.99% or so of coin flips predicted correctly with a possibly feasible experimental setup.

jdods
  • 181
  • 6

2 Answers2

5

If coin tosses had been properly chaotic situations then the amount of information to perfectly predict them would have been infinite in general. However, coins are not as chaotic or random as people think.

(From (Mahadevan and Yong 2011)

If you look at the state space (spin velocity and speed) for a rigid coin, it is divided into stripes of states that produce heads or tails: small deviations inside them do not change the outcome. So the amount of information needed to predict the outcome (assuming no weird effect of the hand or reveal) is limited.

If you demand perfect prediction you will still need infinite information, but being right 99.9999% of the time just requires an error < 1 in a million. This is like reducing the grey areas in the image above to be less than a millionth of the total area. For a given height and spin, this requires about $\log_2(10^6)\approx 19.93$ bits, I think.

Anders Sandberg
  • 34,657
2

In a “deterministic chaotic system,” this is fundamentally impossible, because experimentally-indistinguishable initial conditions yield diverging outcomes.

Whether a coin flip is properly chaotic might be a nontrivial question. However, there are absolutely chaotic parts of the “phase space” of initial conditions. For instance, the coin always has some probability of landing on its edge. The fall direction of such an “inverted pendulum” is a frequent example in introductory treatments of chaotic systems.

rob
  • 96,301