On the motion of a charged particle in a magnetic field

Question

It's often said that a charged particle travelling in a straight line on a plane undergoes a circular trajectory whenever subjected to a uniform static magnetic field perpendicular to the plane.

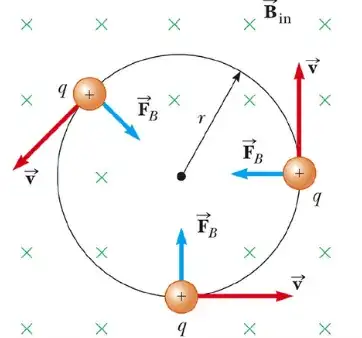
But hold on. A charged particle in a circular motion acts much like a steady current on a loop. And this current produces a magnetic field which will point in the opposite direction of the external one. But in this way, the total net magnetic field diminishes. Consequently, the centripetal force $\mathbf{F}_B=q\mathbf{v}\times\mathbf{B}_{\operatorname{net}}$ will also diminish, and the radius of the Amperian loop will increase. At this point, the $\mathbf{B}_{\operatorname{loop}}$ field produced by this loop is much weaker, according to the formula $\displaystyle B_{\operatorname{loop}}\approx \frac{\mu_0 I}{2\pi R}$, and the external $\mathbf{B}_{\operatorname{in}}$ field is less weakened. The loop will therefore shrink again, and so on.

My point is that the orbit of this particle should oscillate continuously. Is this correct? An oscillating charge produces em waves by the way... are these em waves strong enough to complicate the scenario even further?

Answer 1

Yes indeed particles oscillate around their equilibrium trajectory in a particle accelerator. The emitted radiation is due to the circular orbit itself and is named the synchrotron radiation. What you raise as question is a second order effect compared to this. B(loop) is negligible compared to macroscopic B such as B(synchrotron) or even B(earth) or even B(interstellar).

Please note the relativistic effect which increases the radius R by the relativistic Gamma factor. This effect you should take into account. That's why there is a gradient of B to compensate it in circular accelerators.