When the muon was discovered, it was so unexpected that Rabi's reaction was, "What? Who ordered that?" The muon doesn't play any obvious role in the behavior of protons, neutrons, and electrons. Does the muon substantially affect the functioning of the universe? Does it make sense to imagine a universe where there aren't any muons? Or, is there some feature of our universe that predicts the existence of the muon?
1 Answers
In the Standard Model, the mathematical transformation between “matter” and “antimatter” is called $\newcommand\CP{\mathit{CP}}\CP$. To transform matter to antimatter mathematically, you must “conjugate the charge,” the transformation $C$. (If the matter electron charge is negative, the anti-electron is positive.) You must also invert the parity, $P$, which takes a little more finesse to explain.
The transformation $\CP$ is very nearly a exact symmetry of the universe: antimatter is very nearly exactly the same as matter. If you take anti-protons and anti-electrons to make anti-hydrogen, it has exactly the same energy spectrum as matter hydrogen. If you could make heavier anti-atoms, you would expect anti-chemistry indistinguishable from matter chemistry. Note that the anti-hydrogen experiments have been done starting in the last decade or so. Heavier nuclei would require anti-neutrons and anti-fusion, which may well be an insurmountable technical challenge.
However, $\CP$ is clearly not an exact symmetry of our universe, because we have lots of matter around, but only incidental antimatter. If matter and antimatter were exactly indistinguishable, they would have been created in equal amounts during the radiation-dominated era just after the Big Bang, and there wouldn’t be any matter left for us to build computers out of to type at each other. It may seem to us matter chauvinists that there is a huge matter-antimatter asymmetry. However, we still have enough radiation left from the Big Bang to say that, actually, the matter excess over antimatter was about one part per billion.
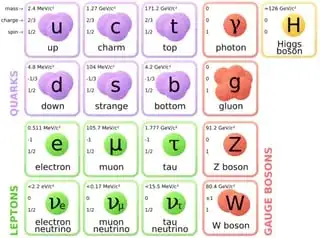
In the Standard Model, we have three “generations” of quarks and three “generations” of leptons:
(We are ignoring the “bosons” in the red and yellow boxes for today.) The different generations are connected to each other by flavor-changing weak interactions. This name both is and isn’t a technical term. The suite of differences that distinguish an electron from a muon or a tau are collectively called the “flavor” of the particle. If flavor-changing interactions weren’t weak, we wouldn’t talk about electron-flavored particles as distinct from muon-flavored particles, because they would be constantly switching names with each other.
Mathematically, the connections between the different flavors are represented by matrices: there is one for quarks and one for neutrinos. Because there are three generations for quarks and for leptons, these are $3\times 3$ matrices, with nine complex numbers each.
And here’s where we have to have the muon — and the tau. The flavor-changing matrices are where $\CP$ violation hides in the Standard Model. And if those flavor matrices were $1\times1$ or $2\times2$, they would not be complicated enough to support a $\CP$-violating phase. If all we had in the universe were the first generation of quarks and leptons, or even the first two generations, the model we have predicts that no matter excess would have persisted after the Big Bang, and the universe would now be completely empty apart from leftover radiation.
The existence of the muon makes the universe complicated enough to support the broken symmetry that is me.
- 96,301