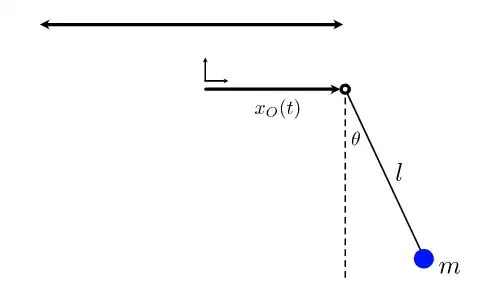
I was trying to find the Eqn. of Motion for the following system (a jiggle pendulum):
Using the Lagrangian and the Euler-Lagrange-Eqn., I ended up with: $$\ddot{\theta} + \frac{g}{l}\sin{\theta} = -\frac{1}{l}\ddot{x_O}\cos{\theta}$$
While it is much easier to solve this eqn. numerically, I was wondering how one would go about solving this analytically. I was trying to solve this eqn. with the following definitions and initial conditions : $$x_O(t) = \sin{(4\pi t)}$$ $$l = 0.2[m]$$ $$\theta(0) = 0$$ $$\dot{\theta}(0) = 0$$
So the eqn. that I have to solve would look like this: $$\ddot{\theta} + 5g\sin{\theta} = 80\pi^2\sin{(4\pi t)}\cos{\theta}\tag{1}$$
But because of my highly limited knowledge, I have hit a roadblock since I have no idea how one would solve a second order nonhomogenous differential eqn. involving trig functions.
During my search on the Internet, I found things like elliptical integrals, complementary functions and particular integrals but I did not quite understand how I should use them.
TL;DR: I would like to solve the second order nonhomogenous diff eqn. marked $(1)$ with the conditions mentioned above it.