With increased binding energy, the rest mass of the products of the reaction is less than the rest mass of the reactants of the reaction, and due to conservation of energy the difference appears as an increase in the kinetic energy of the products compared to the reactants. The decrease in rest mass is due the nucleons in the products being more tightly bound (in lower energy states inside the nucleus) compared to the nucleons in the reactants. The energy "released" as kinetic energy is given by $E = mc^2$. Fission of heavy nuclei as well as fusion of light nuclei result in a decrease in rest mass. Such reactions are exothermic; reactions that increase rest mass are endothermic.
A similar change in rest mass occurs in chemical reactions, but the magnitude is very much less than for nuclear reactions. This change in energy for a chemical reaction is called the energy of formation or the enthalpy of formation in classical thermodynamics; we now know it is a change in rest mass.
Update based on OP follow-up comment/question
The question is “why does binding energy cause mass defect?”.
For a given nucleus, its total binding energy is the energy required to separate the nucleus into its individual nucleons. Energy is required to separate the nucleons because the strong nuclear force inside the nucleus attract the nucleons to each other. A crude classical physics analogy is two masses connected by an elastic spring with the spring not stretched initially; energy is required to pull the masses apart to overcome the force of the stretched spring tending to pull the masses toward one another.
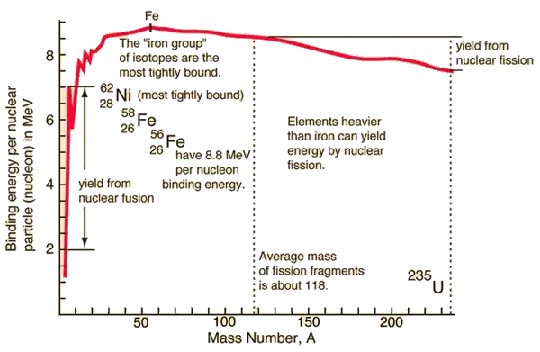
Binding energy is a measure of how tightly the nucleons (protons and neutrons) of a nucleus are bound together. If the binding energy is increased the nucleons are more tightly bound, or in other words the nucleus is in a less energetic internal state; the nucleus has less internal energy. A graph of the average binding energy per nucleon versus the mass number for various nuclei is called a curve of binging energy; a figure below is this curve. The reason for the difference in the average binding energy per nucleon as a function of the nucleus mass number and atomic number has been addressed using models by Brueckner et. al. A simpler model is the liquid-drop model that empirically explains the curve based on: the short range strong nuclear force, an assumption that the strong nuclear force for one nucleon saturates (does not extend) beyond about four adjacent nucleons, and the Coulombic repulsion of protons. Details of these models are complex and are available online and in standard nuclear physics textbooks.
The curve of binding energy indicates that either the fusion of light nuclei or the fission of a heavy nucleus due to a nuclear reaction can result in an increase in the average binging energy per nucleon. An increase in binding energy is a decrease in internal energy. Applying Einstein’s $E = mc^2$ where $E$ is internal energy, $m$ is rest mass, and $c$ the speed of light, the decrease in internal energy is a decrease in rest mass.
Here is a simple example of a change in internal energy. First let’s use a macroscopic viewpoint. Consider a solid that is heated; using the first law of thermodynamics the increase in internal energy of the solid is equal to the heat added. The additional insight due to Einstein is that this increase in internal energy is an increase in the rest mass of the solid. Now, let’s use a microscopic viewpoint. For the solid that is heated, the temperature increases due to the increased kinetic energy of the atoms in the solid. That is, looking inside the solid what we identified as increase in internal energy using the macro viewpoint- not looking inside the solid- is an increase in kinetic energy of the atoms using the micro viewpoint.
Clarification added in italics
Now, let’s consider a nuclear fusion reaction. Let the system be two nuclei that undergo an exothermic reaction: $ a + b -> c$ where $a$ and $b$ are the reactants and $c$ is the product of the reaction. That is, we “move up the curve of binding energy” in this reaction; the reaction increases the average binding energy per nucleon. We observe that the total kinetic energy of $c$ is greater than the total kinetic energy $a$ and $b$. From the macro viewpoint, no heat or work was added to the system (defined here as all the nuclei inside a system boundary) so according to thermodynamics the total internal energy of the system does not change. However, the kinetic energy of the products is greater than that of the reactants, so inside the system the
internal energy of the separate nuclei decreases to account for this increased kinetic energy. Before nuclear reactions were discovered and before Einstein, classical thermodynamics observed exothermic chemical reactions and attributed the required decrease in internal energy of the interacting constituents to “heat (or enthalpy) of formation”; for example, see one of the texts on ‘thermodynamics by Sonntag and Van Wylen. We now know that this classical “heat of formation” used to explain the decrease in internal energy of the constituents is a decrease in rest mass. So, for both a chemical and a nuclear exothermic reaction, the increase in kinetic energy of the products compared to the reactants is accompanied by a decrease in rest mass of the products compared to the reactants. For our fusion example, $c$ has less rest mass than the sum of the rest masses of $a$ and $b$.
For an exothermic nuclear reaction, once the reaction occurs the internal forces (nuclear and Coulombic) reconfigure the nucleons in an overall lower energy state. But, some initial kinetic energy of $a$ and $b$ is required to fuse since we are fusing charged particles and the Coulombic repulsion of the two positively charged nuclei must be overcome before $a$ and $b$ are sufficiently close for the short range strong nuclear force to become dominant. It is sort of like a ball on a high shelf would like to move to the ground due to gravity but some initial energy is required to bump the ball off the shelf.
For a fission reaction using a charge-neutral neutron, for some target nuclei- $235 U$ for example- a very low energy neutron can cause fission. But, you have to cause the free neutron to be released (e.g., from a previous fission) to be available to cause fission
The micro viewpoint for fusion (and fission) is addressed by details in models of nuclear binding mentioned earlier. These models propose explanations for why the binding energy of $c$ is greater than the sum of the binding energies of $a$ and $b$; that is, the nucleons are reconfigured in the reaction to be in overall less energetic states inside the nucleus, reflected on the macro scale as a decrease in internal energy and therefore a decrease in rest mass.