Can one record a speed faster than $c$?

Question

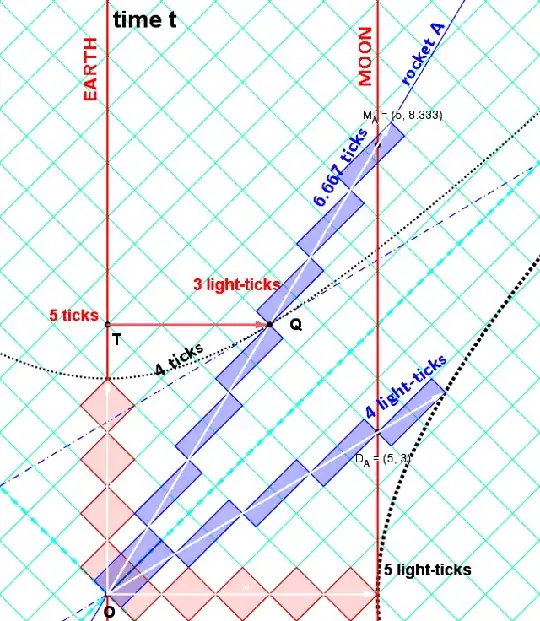
A ship goes to the moon at 0,5 c, the captain will record on his clock about 2 seconds and a half, right?

Now he increases the speed to 0,999 c (or more), thanks to relativity he should record on his clock less than 1 second, and believe he has travelled much faster than light.

Is there something wrong in this example or it is just so?

Edit: it does not matter if the distance has shrunk or not, it is a hard fact that he has travelled 380 000 Km in less then a second

EDIT 2: I am sorry you miss the point of my question. Two or more people are may repeat what SR says, but I maintain that it is an indisputable fact that the captain measure by his clock that he travelled at 2C

MOreover, I add, it is a hard fact that according to SR the very speed of light is NOT invariant, since the captain measures a speed twice as fast if he flashes a torch in the direction of motion and in a normal direction. Can you refute that?

Answer 1

You say:

Edit: it does not matter if the distance has shrunk or not, it is a hard fact that he has travelled 380 000 Km in less then a second

but you need to take care with this statement. It should say:

The captain knows that the Earth observer measured his distance travelled as 380000 km

You can certainly divide the distance measured by Earth by the time measured by the captain and you'll get an answer greater than $c$. The problem is that this is a meaningless result since you are dividing quantities measured in different inertial frames. The result cannot be a speed measured by any observer.

The bottom line is that:

• the Earth observer measured the ship travelling towards the Moon at less than $c$

• the captain measured the Moon travelling towards their ship at less than $c$

So no observer measured a speed greater than $c$.

Answer 2

To support what the earlier answers are saying, consider this "position-vs-time diagram" (spacetime diagram) with time running upwards.

To make the arithmetic easier, I'll use $v=(3/5)c=(0.6)c$ [instead of 0.5c].
$\gamma=\frac{1}{\sqrt{1-(v/c)^2}}=5/4$ and $k=\sqrt{\frac{1+(v/c)}{1-(v/c)}}=2$.

For simplicity, assume that the Earth is an inertial frame and the Moon is at rest relative to the Earth.

In the diagram below, let "1 tick" be "(1/4)second".

• "Length" is the spatial-separation between parallel worldlines.
  Thus, the "proper-length from Earth to the Moon" is [approximately] (5/4=)1.25 light-seconds (5 diamond-widths). This is the length according to the inertial frame where the Earth is at rest.

• "Velocity of an object" according to an observer is the "slope" (="rise of position"/"run in time") $\Delta x/\Delta t$ of the object's worldline, as measured by that observer. .
  Thus, according to the Earth, the Moon is at rest and the Rocket moves with velocity 0.6c since "$3/5=0.6$" and "$5/8.333=0.6$" since the Rocket arrives at the Moon at time 8.333 ticks (2.08 seconds) after traveling 5 light-ticks (1.25 light-seconds).. all measured by the Earth.

Now what does the inertial Rocket measure for its trip to the Moon?
According to special relativity,

• The Moon traveled "-4 light-ticks" as measured by the Rocket. (That the magnitude is shorter than 5 light-ticks is "Length Contraction", as others have said. We have (4 light-ticks)/(5 light-ticks)=$\frac{1}{\gamma}=\frac{1}{(5/4)}$=(4/5).)
  The Rocket's wristwatch reads 6.667 ticks [as measured by the Rocket].
  This implies that the Rocket measures the velocity of the Moon to be "rise/run" $(-4 \mbox{ light-ticks})/(6.667 \mbox{ ticks})=(-0.6)c$, as expected.
  
  As a check, note that $(3)^2-(5)^2=(0)^2-(4)^2$, which is the square-interval from $O$ to $D_A$, where $D_A$ is the event the Rocket says is simultaneous with the separation event $O$.
  
  As another check, note that $(8.333)^2-(5)^2=(6.667)^2-(0)^2$, which is the square-interval from $O$ to $M_A$. "Time-dilation" is the effect that the earth measures the larger value of "8.333 ticks" (as the elapsed Earth-time from $O$ to $M_A$) for the Rocket's "6.666 ticks" as (as the elapsed Rocket-time from $O$ to $M_A$, where the inertial Rocket visits both $O$ and $M_A$). We have (8.333 ticks)/(6.667 ticks)=$\gamma$=(5/4).)
  
  It is important that velocity=rise/run is computed using the observer-measurements of displacements in space and time. One cannot mix Rocket-measurements and EarthMoon-measurements... since the resulting ratios are not the slopes of these worldlines on the position-vs-time diagram drawn by any of these observers.
  
  UPDATE:
  For instance, for the Rocket worldline segment from $O$ to $M_A$ $$\frac{\Delta x_{Earth}}{\Delta t_{Rocket}}=\frac{5\mbox{ light-ticks}}{6.667\mbox{ ticks}}=\frac{3}{4}c=(0.75)c$$ $$\frac{\Delta x_{Rocket}}{\Delta t_{Earth}}=\frac{-4\mbox{ light-ticks}}{8.333\mbox{ ticks}}=\frac{-12}{25}c=(-0.48)c$$ While one can form these and many other ratios, these ratios have no immediate physical interpretation.

---

For other rocket-speeds, values will change according to special relativity.
But one will find that the Moon-velocity in the Rocket-frame is minus the Rocket-Velocity in the [Earth-]Moon-frame... and neither velocity will reach $c$, let alone exceed it, as the other answers have said.

Answer 3

There is something wrong in this example, and it is ... believe he has travelled much faster than light. He has no reason to believe this.

What actually happens (if we expand the phrase "thanks to relativity") is that the ship's captain observes the distance to the Moon shrinking as he speeds up the ship. This phenomenon is known as length contraction, and is how he can get to the Moon in a fraction of a second, but still don't think he has moved faster than light.

Edit:

it is a hard fact that he has travelled 380 000 Km in less then a second

It is not a hard fact that he has travelled 380,000 km in less than a second, and you perceive there's a problem because you have this misconception. Welcome to Relativity - you will meet more of these "weirdness" if you keep studying the theory.