In laser resonators, higher order modes (i.e. TEM01, etc) accumulate phase faster than the fundamental TEM00 mode. This extra phase is called Gouy phase. What is an intuitive explanation of this effect?
Gouy predicted and then experimentally verified the existence of this effect long before the existence of lasers. How did he do it, and what motivated him to think about it?
Several sources link to this paper: S. Feng, H. G. Winful, Physical origin of the Gouy phase shift, Optics Letters, 26, 485 (2001), which tries to give an intuitive explanation of the Gouy phase. Briefly, the point is that convergent waves going through the focus have finite spatial extent in the transverse plane. The uncertainty relation induces then some distribution over the transverse and consequently longitudinal wave vectors. It is claimed that the net effect of this distribution over wave vectors is an overall phase shift, which is larger for higher modes. However to see that one really needs to look into the formulas.
For several years, I have periodically tried to wrap my head around the Gouy phase.
The Gouy phase does not occur only in laser resonators, but it actually comes into play whenever a beam of light is focused.
Addressing your second question (how did Gouy find this crazy phenomenon way back in 1890?), there is a nice discussion of his experiment in this "Progress in Optics" book. Basically Gouy took the same light source (presumably emerging from a pinhole, to give it some degree of spatial coherence) and reflected it with both a curved mirror and a flat mirror. The focusing beam overlapped with the non-focusing beam in a region near the focus and created a circular diffraction pattern. Gouy then looked at the circular diffraction pattern at several different locations, both before and after the focus. He saw that the central region of the diffraction pattern changed from light to dark, indicating a phase shift in the focusing beam - the Gouy phase shift.
So, observing the Gouy phase shift is a relatively easy experiment. Explaining it is not quite so simple.
In a 1980 article titled "Intuitive explanation of the phase anomaly of focused light beams", R. Boyd explains the Gouy phase shift in terms of the difference in propagation of the Gaussian beam and a plane wave, very similar to Gouy's experiment. He shows that the Gouy phase shift can be derived by looking at the path length difference between the "true" path of the light (along path BCD) and the path that would be expected from geometrical optics (path BE).
Gaussian beam optics fundamentally incorporates the idea that, the more tightly light is focused, the larger the divergence of the beam. Since the divergence cannot be infinite, there is a minimum spot size for a given wavelength of light. This behavior of light is a consequence of Heisenberg's uncertainty principle. So, in my understanding, the Gouy phase shift occurs when we compare the "quantum" behavior of light with what we would expect from geometrical optics.
To take this explanation one step further, we can consider higher-order modes. These modes don't reach as tight of a focus as a simple Gaussian beam. Now, the difference between BCD and BE is even larger.
Feng and Winful's paper (cited above by Igor Ivanov) gives a good explanation.
A plane wave is defined by a single wavevector $\mathbf{k}$, so its wavefronts are equally spaced. The plane waves composing a finite monochromatic beam -- the beam's angular spectrum (AS) -- all have different $\bf{k}$, but all have the same magnitude $k_0=\omega_0/c$. Thus, the further off-axis the $\mathbf{k}$ of a plane wave in the AS, the smaller is its axial component $k_z$; the axial-plane-wave contribution ($\mathbf{k_0}=k_0\mathbf{\hat{z}}$) has the maximum value $k_z=k_0$. F&W find an effective $k_z$ by averaging over all $\mathbf{k}$ in the AS; naturally, the result is less than $k_0$, and the difference corresponds to the Gouy phase $\zeta$. (It will be useful later to note that the averaging over $k_z$ can be recast as averaging over $k_x$ and $k_y$ instead, again because all AS components have the same magnitude $k_0$.)
I think that's a complete explanation of why $\zeta$ occurs, but we can also try to get some more details:
A tighter focus means a larger beam divergence, so larger off-axis AS contributions. $\zeta(z)$ accumulates faster for tightly focused beams (e.g., it reaches $\frac{\pi}{4}$ within one Rayleigh range of a Gaussian beam waist).
Despite (1), $\zeta(\infty)$ does not depend on waist size, only on the beam's $M^2$, or uncertainty product. I don't have a good intuitive explanation of this.
Finally, to address the original question: why do higher-order modes have larger Gouy phase? The answer is simply that they have higher off-axis contributions in their ASs. To see this, note that the a TEM mode's amplitude profile acquires more "features" for increasing mode order: $\text{TEM}_{mn}$ has $m$ $(n)$ nodes in the $x$ $(y)$ direction. The spatial frequencies required to create these features correspond to off-axis plane waves in the AS. So if we take a Gaussian and a higher-order mode, both with the same beam waist, the higher-order mode has higher off-axis plane-wave content, and will therefore acquire a bigger phase shift after finite propagation.
Other questions seem to be trying to answer the simpler question of why a Gaussian mode has a Gouy phase (i.e. compared to plane-waves), rather than the actual question being asked as to why higher order modes have a faster accumulation of Gouy phase (i.e. why phase for the $n^{th}$ order mode has a phase $\Delta\phi=n\psi(z)$ higher than the $0^{th}$ order Gouy phase of $\psi(z)$), which I will try to answer.
For me, an intuitive understanding comes from understanding what we mean by "modes." A mode is a configuration of the field that doesn't change upon propagation, or rather only changes trivially via e.g. a phase or a rescaling. So upon propagation a "mode" is a field that transforms like $$U(x) \to U(x')e^{-\phi}.$$
Modes are highly dependent on the physics of wave propagation. The first thing
to note is that propagation from $z=0$ to the far-field $z\to\infty$ is given
by a Fourier transform. Therefore the propagation from $z=-\infty$ to
$z=\infty$ is given by two Fourier Transforms. However, two Fourier transforms
just flip the field, i.e. if $U(x)$ is the field at some transverse point $x$,
then Fourier transforming twice just gives $\mathcal F(\mathcal F(U(x))) =
\mathcal P U(x)= U(-x)$, where $\mathcal F$ is the Fourier operator and
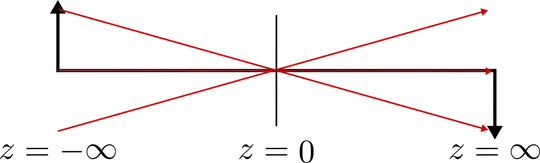
$\mathcal P$ is the parity operator. A ray-picture of propagation from $z=
-\infty\to\infty$ is given in the image below. This can also be thought of by
the picture that at infinity, all sources look like spherical waves.
Now applying the parity operator twice gives the same mode $\mathcal P\mathcal P U(x) = \mathcal PU(-x) = U(x)$. There are only two types of modes that obey the parity operator, even and odd functions, i.e. $$ \mathcal PU_\text{even}(x) = U_\text{even}(x),$$ or $$\mathcal PU_\text{odd}(x) = -U_\text{odd}(x).$$ This is equivalent to saying that the only phases that a mode can accumulate are $$\mathcal P U_n(x) = e^{i\pi n}U(x),$$ where $n$ is an integer representing even or odd modes when $n$ is likewise an even or odd number.
So physically we see that a "mode," $U(x)$ is either an even or odd function which simply flips $U(x)\to U(-x)$ when going from $z=-\infty\to\infty$, which we can represent as a phase $e^{i\pi n}$. The second piece of physics we add is the fact that propagation is continuous. Therefore, a "mode" acquires a half the phase from $z=-\infty\to 0$ and half the phase from $z=0\to\infty$. Therefore, all modes aquire a phase difference from $z=0\to\infty$ of $e^{i\pi n/2}$, for some integer $n$.
Mathematically, the Fourier transform $\mathcal F$ is simply the square root of the parity operator $\mathcal P$ (and the inverse Fourier transform can be thought of as the negative root). If you were to try to mathematically solve for eigenmodes of $\mathcal F$, you would find modes with exactly the $e^{i\pi n/2}$ eigenvalues from above. You can actually take this one step further and consider the Fractional Fourier transform, which is just the continuous version of $\mathcal F$ where $\pi/2$ is replaced by a continuous parameter $\alpha$. The Gaussian modes of propagation are also "modes" of this continuous operator (for the obvious reason that propagation is continuous). For paraxial propagation $\alpha = \text{arctan}(z/z_R)$, which gives exactly the Guoy phase as a function of $z$, i.e. $ e^{i\alpha n} = \text{exp}[in\text{arctan}(z/z_R)]=\psi(z).$
Therefore the intuitive answer for what is the Guoy phase and why is it different for different modes is the fact that propagation causes fields to flip (through the origin) and "modes" are defined in terms of fields where this geometric flipping can be represented by a phase, and different phases are what actually defines different modes.
A naive explanation says that a beam after its focal point is inverted, not only in the sense of its spatial distribution but also in the sense of the direction of the electrical field vector (minus sign = adding $\pi$ to the phase). It's perfectly compatible with the fact why even beam profiles change the phase by $\pi$ and odd do not.
However, this explanations says nothing about behaviour of the phase near the focal point.
