In units where $c=1$, the Lorentz transformations are
\begin{align}
\bar{t}&=\frac{t-vx}{\sqrt{1-v^2}},\quad\bar{x}=\frac{x-vt}{\sqrt{1-v^2}}.
\end{align}
By following a similar process to what I described in this answer, I leave it to you to verify the following facts: in the $(t,x)$ coordinate system,
- The $\bar{t}$-axis is drawn at a slope of $\frac{1}{v}$, while the $\bar{x}$-axis is drawn at a slope of $v$
- level sets of $t$ are horizontal lines, while level sets of $\bar{t}$ are straight lines of slope $v$
- level sets of $x$ are vertical lines while level sets of $\bar{x}$ are straight lines of slope $\frac{1}{v}$
- $-t^2+x^2=-\bar{t}^2+\bar{x}^2$.
Now some basic facts about hyperbolas: the set of points for which $-t^2+x^2=k$ (equivalently $-\bar{t}^2+\bar{x}^2=k$), where $k\in\Bbb{R}$ is a constant fall into three categories:
- $k>0$, in which case the hyperbola opens left-right
- $k=0$, which are straight lines $t=\pm x$ (degenerate hyperbolas)
- $k<0$, in which case the hyperbola opens top-bottom,
and obviously through each point in the plane, there is a unique such hyperbola passing through that point.
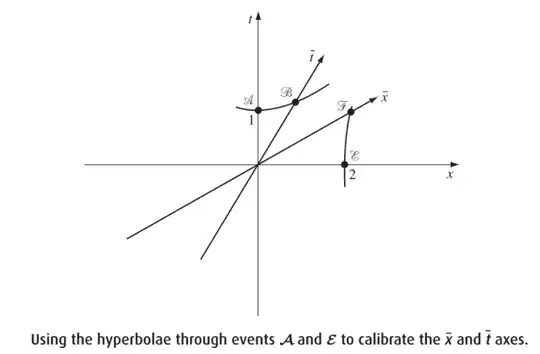
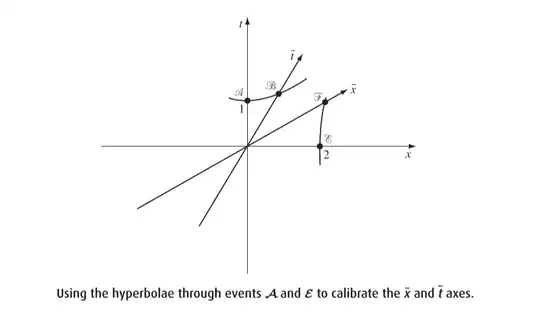
I'm not sure about the purpose of mentioning this calibration procedure using hyperbolas. Generally, when we calibrate something, it means we have some fixed scale, and we're using that to set the scale of something else. But here, we already know the full relationship between $(t,x)$ and $(\bar{t},\bar{x})$, so I'm not sure about the purpose of this. In any case, here's what we can say geometrically: if we consider the point $\mathscr{A}$ with $t(\mathscr{A})=1,x(\mathscr{A})=0$, then you can draw the unique hyperbola through the point $\mathscr{A}$ (i.e the hyperbola with $k=-(1)^2+0^2=-1$). This hyperbola will intersect the $\bar{t}$-axis at a unique point $\mathscr{B}$ which has $\bar{t}(\mathscr{B})=1,\bar{x}(\mathscr{B})=0$. So, by starting from $(t,x)=(1,0)$ we managed to geometrically figure out where the point with $(\bar{t},\bar{x})=(1,0)$ lies. We can keep going: start with the point having $(t,x)=(2,0)$ we can geometrically figure out the point with $(\bar{t},\bar{x})=(2,0)$, next we can start with the point with $(t,x)=(3,0)$ we can figure out where $(\bar{t},\bar{x})=(3,0)$ is and so on.
Similarly, starting with the point such that $(t,x)=(0,1)$ we can draw the hyperbola and figure out where $(\bar{t},\bar{x})=(0,1)$ is, and then so on with $(0,2),(0,3)$ etc. So, by having the scale markings on the $t$ and $x$ axes, we can geometrically figure out the scale markings on the $\bar{t}$ and $\bar{x}$ axes. Having said this, and while this geometry is nice on its own, it doesn't tell you anything which the Lorentz transformations do not already tell you. Hopefully this answers your questions 1 and 2.
Finally, here's a quibble with your comment following your question 1:
... I think it means to establish simultaneity between two different reference frames, but, I'd like a second confirmation as well.
No, this makes no sense. Simultaneity is not a notion to be related between two observers. Simultaneity is a concept within one observer's frame. In the $(t,x)$ coordinate system, simultaneity is described by the level sets of $t$. Or more precisely, we say two events $p,q$ in the spacetime are simultaneous with respect to $(t,x)$ if and only if they lie in the same level set of $t$ (i.e if and only if $t(p)=t(q)$). In the case we're considering, these are the horizontal lines, as I mentioned above. We can obviously make an analogous definition for the barred coordinates: two events $p,q$ are said to be simultaneous with respect to $(\bar{t},\bar{x})$ if and only if they lie in the same level set of $\bar{t}$ (i.e $\bar{t}(p)=\bar{t}(q)$), and geometrically this happens if and only if they lie on the same straight line of slope $v$.