Product of Lorentz invariant factors may be Lorentz non-invariant

Question

I'm evaluating an integral and I have three cases to consider. The result of that integral must be Lorentz invariant and independent of center-of-mass momentum. One of the cases I'm certain is in fact not Lorentz invariant despite being constructed of nothing but Lorentz invariant factors. The integrand is not independent of center-of-mass momentum. The integrand is constructed of a potential and the propagator of 2 particles. Allow the following definitions:

Center of mass 4-momentum: $P^\mu=q_+^\mu+q_-^\mu=(\sqrt{s+P^2}/4,\vec P)$

Relative 4-momentum: $2k^\mu=q_+^\mu-q_-^\mu=(k_0,\vec k)$

On-shell energy: $\omega_\pm=\sqrt{M^2+q_\pm^2}=\sqrt{M^2+(\vec P/2\pm\vec k)^2} $

From these definitions: $q_\pm^\mu=\frac12P^\mu\pm k^\mu$

The potential is given to be either: $$v(k^\mu)=\left(\frac{2\Lambda^2}{2\Lambda^2+|4k^\mu k_\mu|}\right)^2=\left(\frac{2\Lambda^2}{2\Lambda^2+|4k_0^2-4\vec k^2|}\right)^2\\ v(\vec P,\vec k)=\left(\frac{2\Lambda^2}{2\Lambda^2+|(\omega_+-\omega_-)^2-4\vec k^2|}\right)^2$$ The 2-particle propagator is given to be either: $$ImG_{12}(P^\mu,\vec k)=-\int\frac{dk_0}{2\pi}\rho(q_+^\mu)\rho(q_-^\mu)\quad\quad\rho(q^\mu)=Im\left(\frac{2M}{q^\mu q_\mu-M^2+i\Gamma\sqrt{q^\mu q_\mu}\theta(q_0-|\vec q|)}\right)\\ Im\tilde{G}_{12}(P^\mu,\vec k)=Im\left(\frac{2M^2(\omega_++\omega_-)}{\omega_+\omega_-(s+P^2-(\omega_++\omega_-)^2+iM\Gamma(s))}\right)$$ Given the construction of the first potential, it is Lorentz invariant. The second potential is also Lorentz invariant as it comes from the first and the relative energy is put on-shell. The first two-particle propagator is Lorentz invariant by construction. Its width is constructed to constrain it to time-like particles only. If I allow the width to be constant, then the $k_0$ limits of integration go from $-P_0/2$ to $P_0/2$ and that is not Lorentz invariant as the integrand gains more and more area with increasing center-of-mass momentum. The second is derived from the first in an energy reduction such that it is also Lorentz invariant. If you take its zero width limit, you'll find it to be $\frac{2 M^2(\omega_++\omega_-)}{\pi\omega_+\omega_-}\delta(s+P^2-(\omega_++\omega_-)^2)$ or energy conservation.

I have numerically evaluated the following integrals and determined if they do or do not vary with respect to center of mass momentum: $$\frac d{dP}\int\frac{d^4k}{(2\pi)^4}\rho(q_+^\mu)\rho(q_-^\mu)v(k^\mu)=0\\ \frac d{dP}\int\frac{d^3k}{(2\pi)^3}Im\tilde{G}_{12}(P^\mu,\vec k)v(\vec P,\vec k)=0\\ \frac d{dP}\int\frac{d^3k}{(2\pi)^3}ImG_{12}(P^\mu,\vec k)v(\vec P,\vec k)\neq0$$ 1

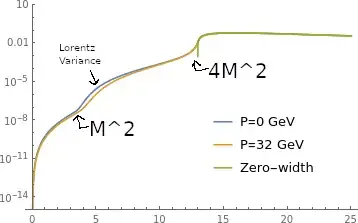
Despite all factors being Lorentz invariant, the third integral is dependent on center-of-mass momentum. With the results numerically evaluated and plotted above on a log plot, it is visually beyond obvious that Lorentz invariance is violated below the two-particle threshold ($s<4M^2$). It is not obvious above the two-particle threshold as the on-shell contributions of $ImG_{12}$ dominate the result and so it might as well be the zero-width limit which are Lorentz invariant. Doing a zero-width analysis on all 3 yields $$-\frac{\Lambda^4M^2}{\pi(s-4M^2+2\Lambda^2)^2}\sqrt{1-\frac{4M^2}s}$$ because the zero-width is the on-shell. The problem must be off-shell. The best explanation that I have is that $v(\vec P,\vec k)$ knows nothing about the off-shell energy contributions of $ImG_{12}(P^\mu,\vec k)$. The next best explanation that I have is that the Lorentz transformations of the two factors is different in a such a way that the product of the two is not Lorentz invariant. Neither of these explanations is sufficient for my advisor as he is firmly of the belief that the product of Lorentz invariant quantities must also be Lorentz invariant. Is there a way to prove that the product of Lorentz invariant factors is not Lorentz invariant either in general or this product in particular?

Edit 1: In Prahar's answer to nosumable's question, he states that $(k_\mu\partial_{k^\nu}-k_\nu\partial_{k^\mu})f(k^\mu)=0$ for a Lorentz invariant scalar function. I've tested it on a few of my functions and it checks out as a test for Lorentz invariance so long as the signs are done right. That's all well and good, but I have $f(P^\mu,k^\mu)$. An extension from a scalar function of one Lorentz covariant 4-vector to a scalar function of two Lorentz covariant 4-vectors is all I need.

Edit 2: The natural extension does not appear to be the test of Lorentz invariance as it failed to pass something that known to be Lorentz invariant. The natural extension I came up with is $(k_\mu\partial_{k^\nu}-k_\nu\partial_{k^\mu})(P_\sigma\partial_{P^\rho}-P_\rho\partial_{P^\sigma})f(P^\mu,k^\mu)$. It failed to pass this expression using just the spatial indices as it doesn't have a 0 index: $$-\frac{q_+^\mu q_{-\mu}+M^2}{M^2}=-\frac{\omega_+\omega_--P^2/4+k^2+M^2}{M^2}$$ It will pass it if the relative 3-momentum or center-of-mass 3-momentum is zero, but those aren't the interesting cases.

Answer 1

I have an answer. After banging my head off of chain rule and change of variables non-sense all day, I recalled that 0+0=0 and $\frac{d}{dx}xy=y$. That means that the Lorentz test for one 4-vector doesn't care about the test for the other 4-vector. The test for one 4-vector is given as $$(k_\mu\partial_{k^\nu}-k_\nu\partial_{k^\mu})f(k)=0$$

This suggests that the test for two 4-vectors is $$(P_\mu\partial_{P^\nu}-P_\nu\partial_{P^\mu}+k_\mu\partial_{k^\nu}-k_\nu\partial_{k^\mu})f(P,k)=0$$

That probably works, but I also need it to work on-shell and turning $\partial_{k^0}$ to on-shell is not something I want to deal with. In the question, I state that $k_0=(\omega_+-\omega_-)/2$. But it is also $\sqrt{s/4-\omega_+\omega_-}$ and to satisfy the simultaneous on-shell condition $q_{+\mu}q_+^\mu=q_{-\mu}q_-^\mu=M^2$ it can be shown that $k_0=\frac P2\cos\theta\sqrt{\frac{4M^2-s}{s+P^2\sin^2\theta}}$. Given these different forms, I didn't want to have to deal with it. To avoid that nonsense, I instead elected to use the particle 4-vectors. $$(q_{+\mu}\partial_{q_+^\nu}-q_{+\nu}\partial_{q_+^\mu}+q_{-\mu}\partial_{q_-^\nu}-q_{-\nu}\partial_{q_-^\mu})f(q_+,q_-)=0\\ (q_{+0}\partial_{q_+^i}+q_{+i}\partial_{q_+^0}+q_{-0}\partial_{q_-^i}+q_{-i}\partial_{q_-^0})f(q_+,q_-)=0\\ (q_{+i}\partial_{q_+^j}-q_{+j}\partial_{q_+^i}+q_{-i}\partial_{q_-^j}-q_{-j}\partial_{q_-^i})f(q_+,q_-)=0\\$$ They pass the following expression as Lorentz invariant: $$\frac{2M^2\Gamma}{(q_+^\mu q_{+\mu}-M^2)^2+M^2\Gamma^2}\frac{2M^2\Gamma}{(q_-^\mu q_{-\mu}-M^2)^2+M^2\Gamma^2}\left(\frac{\Lambda^4}{\Lambda^4+((q_+^\mu-q_-^\mu)(q_{+\mu}-q_{-\mu}))^2}\right)^2$$ That's nice for the off-shell. To the on-shell case where I need to put $\partial_{q_\pm^0}$ on-shell. $$\frac{\partial f}{\partial q^0}=\frac{\partial f}{\partial q^i}\frac{\partial q^i}{\partial q^0}\\ q_0=\sqrt{M^2+q_i^2}\Rightarrow dq_0=-\frac{dq_i}{2\sqrt{M^2+q_i^2}}\\ \frac{\partial f}{\partial q^0}=-2\sqrt{M^2+q_i^2}\frac{\partial f}{\partial q^i}$$ That makes the on-shell version of the test $$(q_{+0}\partial_{q_+^i}-2\omega_+q_{+i}\partial_{q_+^i}+q_{-0}\partial_{q_-^i}-2\omega_-q_{-i}\partial_{q_-^i})f(q_+,q_-)=0\\ (q_{+i}\partial_{q_+^j}-q_{+j}\partial_{q_+^i}+q_{-i}\partial_{q_-^j}-q_{-j}\partial_{q_-^i})f(q_+,q_-)=0\\$$ They pass the following expression as Lorentz invariant: $$\frac{2M^2\Gamma}{(\omega_+^2-q_{+i}^2-M^2)^2+M^2\Gamma^2}\frac{2M^2\Gamma}{(\omega_-^2-q_{-i}^2-M^2)^2+M^2\Gamma^2}\left(\frac{\Lambda^4}{\Lambda^4+((\omega_+-\omega_-)^2-(q_{+i}-q_{-i})^2)^2}\right)^2$$ Both tests failed the following expression as not Lorentz invariant: $$\frac{2M^2\Gamma}{(q_+^\mu q_{+\mu}-M^2)^2+M^2\Gamma^2}\frac{2M^2\Gamma}{(q_-^\mu q_{-\mu}-M^2)^2+M^2\Gamma^2}\left(\frac{\Lambda^4}{\Lambda^4+((\omega_+-\omega_-)^2-(q_{+i}-q_{-i})^2)^2}\right)^2$$ The temporal condition is what failed the expression. I suspect that if it wasn't rotationally symmetric, then the spatial condition would have failed it. Given the above plots having fairly small error, then I would expect the error that it failed by to also be small. The error expressions not small things to write down, but, for a sample size of 2, they are small. If I put the error on-shell, then the on-shell error becomes 0 and the off-shell is $-2.44\times10^{-9}$. Plugging in somewhat arbitrary values on the error expressions, I get $3.18\times10^{-10}$ for the on-shell and $1.29\times10^{-10}$ for the off-shell. I get similar results for the potential that I asked the question with except putting the error on-shell made both errors go to 0. The only problem to reporting the actual numbers is taking the derivative of abs().