How does gravity make us rotate about the rotation axis of earth?

Question

A body at the surface of earth experiences at least two obvious forces - gravity and its weight (normal of the surface). Both of these forces act on the radial axis that goes through the center of earth.

But for a body to rotate about the rotation axis of earth, it needs to accelerate towards the said axis. This acceleration is perpendicular to this axis and maintains an angle (equal to the latitude) with the radial axis where the forces act along.

My question is, how does these forces create this acceleration and nothing else. What am I missing?

Answer 1

Gravity always acts to the center of the Earth (if you assume the Earth as a sphere). The rotation (which has nothing to do with gravity) creates an additional centrifugal force acting outwards perpendicular to the rotation axis. This means you will weigh a little bit less the more you go from the pole to the equator.

I have given the mathematical derivation of the direction of gravity on the Earth's surface in an answer to a related question. The result is that for mid-latitudes this direction misses the center of the Earth by about 0.2 deg, half of which is due to ellipsoidal shape of the Earth and the other half due to the centrifugal force because of the rotation. This is consistent with published figures.

Answer 2

The Earth rotates because it formed in the accretion disk of a cloud of hydrogen that collapsed down from mutual gravity and needed to conserve its angular momentum. It continues to rotate because of inertia.

Answer 3

The force of gravity acts vertically downward towards the centre of the Earth. If you are neither at the poles or the equator, but at some arbitrary latitude as shown in your diagrams, then you can represent the gravitational force as having two components, one directed towards the Earth's axis of rotation and the other directed parallel to it. It is the component directed towards the Earth's axis that provides the centripetal attraction to keep you in motion in a circle.

The centrifugal effect is quite small, ranging from nothing at the poles to about a 0.5% reduction in the acceleration due to gravity at the equator, and it acts normal to the Earth's axis of rotation.

At the poles and at the equator the effect is easy to understand- at the former it doesn't exist and at the latter the centrifugal effect points directly away from the Earth's centre (more or less) and so just reduces your weight straightforwardly.

At other points on the Earth's surface the impact of the centrifugal effect is to reduce the component of your weight acting towards the Earth's axis, without changing the component that acts parallel to the Earth's axis, which causes the effective direction of your weight to change fractionally, which would tend to pull you towards the Earth's equatorial plane. However, the effect is very small compared with the force of friction that keeps you on your feet, so in practice you wouldn't notice it.

Answer 4

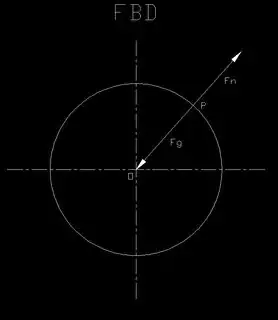
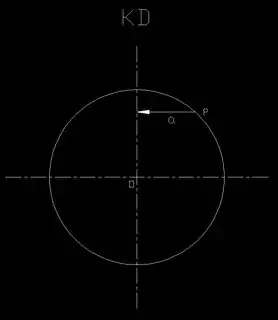
Both of these forces act on the radial axis that goes through the center of earth. … My question is, how does these forces create this acceleration and nothing else. What am I missing?

You are missing the fact that neither of those forces actually go through the center of the earth.

First, the contact force between the earth and the body has both a vertical and a horizontal component. This horizontal component arises from static friction and is often larger than the centripetal acceleration. This is the force, for example, that keeps the object from sliding down a hill or sliding around from a light breeze. It also provides whatever small force is needed for the centripetal motion.

Second, the earth is not uniform. There are variations in density and local features like mountains and so forth. All of these perturb the local gravitational vector so that it does not actually point towards the center of the earth. If you took those deviations and constructed a shape such that the surface is everywhere perpendicular to the local gravitational vector, that shape is called the geoid. That shape is, in some sense, the actual shape of the earth, and on it there would be no static friction. The force for the centripetal motion would come from the sum of the normal force and the local gravitational force, neither of which would necessarily point towards the center.

Now, suppose that we were not on the earth, but rather on a perfectly uniform density planet with the same mass and angular velocity as the earth. Suppose further that the planet is formed of some fluid so that there are no mountains or hills and that there is no wind or moons so there are no waves or tides. Such a planet would have everywhere a gravitational vector that points exactly to the center of the earth, and since it is a fluid the surface is everywhere normal to the local gravitational force so there is no horizontal forces. Now, on such an idealized planet the geoid would be an ellipsoid, and although the gravitational force would be through the geometric center, the normal force would not except at the equator and the poles. The sum of the center-directed gravitational force and the off-center normal force would give the required centripetal force.

Finally, suppose that the idealized planet was not a fluid ellipsoid, but a solid sphere, and suppose that it were frictionless. In that case both the normal force and the gravitational force would point perfectly towards the center, and with no friction the net force could not cause only the desired centripetal motion. Instead, the body would begin to slide towards the equator. This is the scenario you were analyzing. The fact that we don’t observe this behavior is because the earth is not a uniform frictionless sphere.

Answer 5

Friction between the body and earths surface provides a tangential force necessary to get a body rotating around earths axis in the first place.