My View: I think that if the sun were only force acting on earth (as a centripetal force), the earth would have a circular orbit. Since other planets also exist , there also exists gravitational force between interplanetary bodies. This maybe would cause a elliptical orbit. Is the the right answer to this?
Specific question: Since the cycle of revolution is different for different planets , shouldn't there be change in the shape of the orbit of the Earth?
In physics one uses mathematics to solve these problems. There are some misunderstandings.
I believe that if the sun were only force acting on earth (as a centripetal force), the earth would have a circular orbit. Since other planets also exist , there also exists gravitational force between interplanetary bodies. This causes a elliptical orbit.
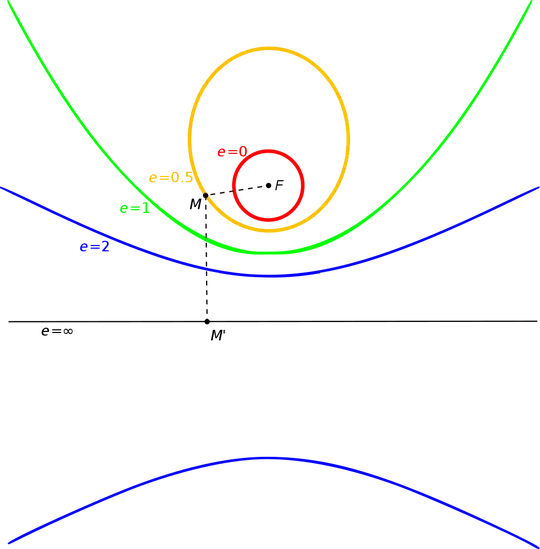
This is not true. The solution of the orbits for two bodies is exact for the classical gravitational force, and they are the conic sections. Bound states are either ellipses or circles.
When more than two bodies enter the gravitational equation the total solutions are not exact, they have to be numerically calculated . This is successfully done in solar system simulators, for example here.
They may look like circles, but that is because of the very much larger mass of the sun with respect to the planets.The functions themselves are ellipses
What shape describes the orbits of planets in our solar system?
In the 17th century Johannes Kepler showed that planetary orbits are ellipses. Newton’s laws of motion confirmed this. Modelling planetary orbits as ellipses is quite accurate. In fact NASA publish the orbital parameters which define the ellipses for the orbits of the planets.
As StrongLizard points out in the comments, the experimental fact that the orbits are elliptical, discovered by Kepler, led to the theory of gravitation by Newton that gives the mathematics . In the mathematics, all objects in the solar system are revolving around the center of the total mass of the solar system, even the sun. Their revolutions is elliptical because it is the ellipse that fits the data. That's the way they were caught and bound in the solar system ( or evolved into bound masses around their star at the development of galaxies in the cosmological model). –
To calculate the orbital motion of the planets, refer to Kepler's laws. For the shape of the trajectory of the planets, it is especially the conservation of angular momentum that interests us: \begin{equation} \vec{L} = \vec{r} \times \vec{p} \end{equation} This formula implies that the speed of the planets is proportional to the force applied to them, thus their proximity to the sun.
Depending of the force they initially have, trajectories of the planets are conic sections:
As our planets do not have too much kinetic energy, they will describe elliptical trajectories, which are characterized by an eccentricity smaller than 1. The circle has an eccentricity of 0, this is an extreme case which is never observed.
You can learn more about conic sections there.
Have a nice Sunday !
I believe that if the sun were only force acting on earth (as a centripetal force), the earth would have a circular orbit.
Many once thought as you did. I won't go through the full proof that Newton's laws of motion and gravitation imply the orbit is in general an ellipse, but let me give an intuitive reason why a circle isn't right in general.
A circular orbit has only one parameter, its radius. But since Newton's second law mentions acceleration, which is a second-order rate of change, it takes two parameters to describe a path, e.g. the position and velocity at one instant. Effectively, we need two "radii", an ellipse's semi-axes.
This is actually related to another common point of confusion concerning gravity. People often ask why planets don't fall into the Sun the way an object will fall to Earth if you release it. The two-parameter aspect of the path makes the relative directions of velocity and acceleration important, and only the latter is "down". When you drop something, it falls straight if these vectors are parallel; for a circular orbit, they'd have to be perpendicular. In practice, they're something in between, like a ball thrown in an arc.
