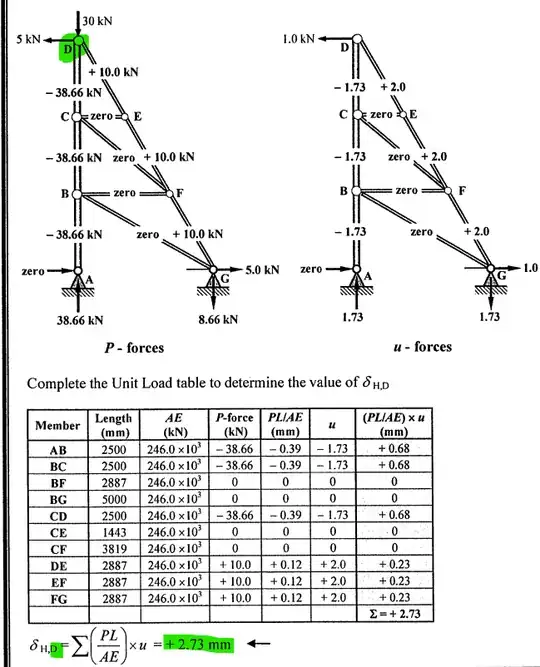
Dear Readers, why doesnt the deflection formula depend on moment of inertia (I) or even the second momnet of area that are responsible for the cross-sectional shape of beam. Does that mean in the example below, for a round cross-sectional area vs a triangular cross-sectional are have the same amount of deflection? I feel so confused :)
1 Answers
The stiffness (and hence deflection) of each member is
$$ k = \frac{E A}{L}$$
You can clearly see this factor in the deflection formula. The shape of the cross section does not matter, as only the area $A$ and elastic modulus $E$ determine the elastic properties of the section.
This is because each member is two force member carrying only axial force. No side load or moments transmit through these truss members (for simplicity) and hence the shear and bending response is willfully ignored here. The ends of each members is said to be pinned in this analysis, which means can freely rotate.
In real life, the joints between members would not allow any rotation, thus needing to carry bending moments to enforce this constraint. Then each member would need to consider both the axial stiffness $E A/L$ as well as the bending stiffness $3 E I/L^3$.
Related Questions/Answers
- 3,765